I Quadrilateri: Tipi e Caratteristiche
In geometria, i quadrilateri sono figure con quattro lati e quattro angoli. Anche se hanno tutti quattro lati, i quadrilateri possono essere molto diversi tra loro. Oggi vedremo insieme i quadrilateri più importanti, con le loro caratteristiche specifiche, per imparare a riconoscerli facilmente.
1. Trapezio
Il trapezio è un quadrilatero che ha almeno una coppia di lati opposti paralleli. Questi lati paralleli vengono chiamati basi. I trapezi sono una categoria molto varia e hanno diverse sottoclassi, come vedremo.
2. Trapezio rettangolo
Il trapezio rettangolo è un tipo particolare di trapezio in cui due angoli sono retti (cioè misurano 90°). Questa caratteristica rende il trapezio rettangolo simile a un rettangolo in una delle sue metà. Si distingue dagli altri trapezi per la presenza di un angolo retto, che lo rende particolarmente facile da identificare.
3. Trapezio isoscele
Il trapezio isoscele è un altro tipo speciale di trapezio. In questo caso, i lati non paralleli (chiamati lati obliqui) sono di uguale lunghezza, e gli angoli alla base sono uguali tra loro. Questa simmetria fa sì che il trapezio isoscele abbia un aspetto armonioso e spesso venga usato nell’architettura e nel design.
4. Parallelogramma
Il parallelogramma è un quadrilatero in cui entrambi i lati opposti sono paralleli e di uguale lunghezza. In altre parole, i lati opposti sono paralleli tra loro e hanno la stessa misura. Un parallelogramma può avere forme diverse, a seconda degli angoli e dei lati, e infatti anche il rettangolo e il rombo sono dei parallelogrammi (con caratteristiche aggiuntive).
5. Rombo
Il rombo è un tipo particolare di parallelogramma. Ha tutti e quattro i lati di uguale lunghezza e le sue diagonali sono perpendicolari tra loro (si incontrano formando un angolo retto). Anche se non ha necessariamente angoli retti, è molto simile al quadrato. Il rombo si trova spesso in natura e nei disegni decorativi grazie alla sua simmetria.
6. Rettangolo
Il rettangolo è un altro tipo speciale di parallelogramma. In un rettangolo, i quattro angoli sono tutti retti (di 90°) e i lati opposti sono paralleli e uguali. Il rettangolo è una delle forme più comuni e si trova ovunque: dagli schermi dei dispositivi alle finestre, ai tavoli, e così via. È facile da riconoscere per la sua forma allungata e per gli angoli retti.
7. Quadrato
Infine, abbiamo il quadrato, che è un quadrilatero davvero speciale: è sia un rettangolo sia un rombo. Questo significa che ha sia quattro angoli retti (come un rettangolo) sia tutti i lati uguali (come un rombo). Il quadrato ha quindi tutte le caratteristiche degli altri tipi di quadrilateri, il che lo rende una figura perfettamente simmetrica e regolare. Grazie alla sua forma, è molto facile da riconoscere ed è considerato il “re” dei quadrilateri.
Riepilogo
Ecco un modo semplice per ricordare le differenze:
- Il trapezio ha almeno una coppia di lati paralleli.
- Il trapezio rettangolo ha due angoli retti.
- Il trapezio isoscele ha i lati obliqui uguali.
- Il parallelogramma ha entrambe le coppie di lati opposti paralleli.
- Il rombo ha tutti i lati uguali e diagonali perpendicolari.
- Il rettangolo ha quattro angoli retti.
- Il quadrato è un rettangolo con tutti i lati uguali.
Questa guida vi aiuterà a riconoscere i quadrilateri e a distinguerli con facilità. Buono studio!
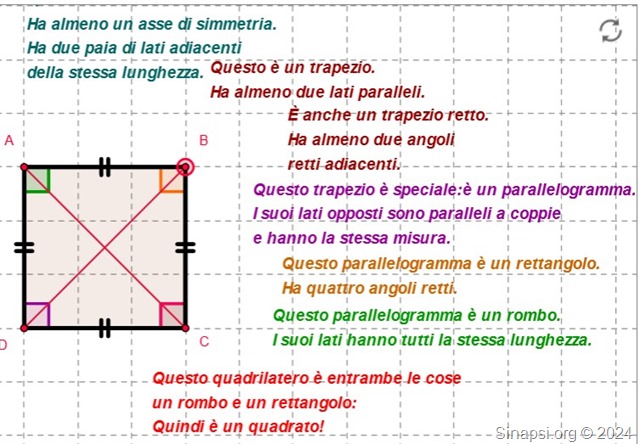
Qui sotto puoi interagire con GeoGebra e muovere i vertici del quadrilatero per visualizzare le caratteristiche che hai appena imparato.


