Il sito di GeoGebra si è arricchito di nuove interessanti funzioni.
GeoGebra è molto di più di una raccolta di strumenti gratuiti per fare matematica. È una piattaforma che mette in contatto insegnanti, appassionati e studenti, offrendo loro un modo nuovo per esplorare e imparare la matematica.
La sezione Math Practice, sviluppata in collaborazione con Graspable Math consente agli studenti di esercitarsi in aritmetica e algebra in modo interattivo, ottenendo un feedback immediato sulle operazioni svolte.
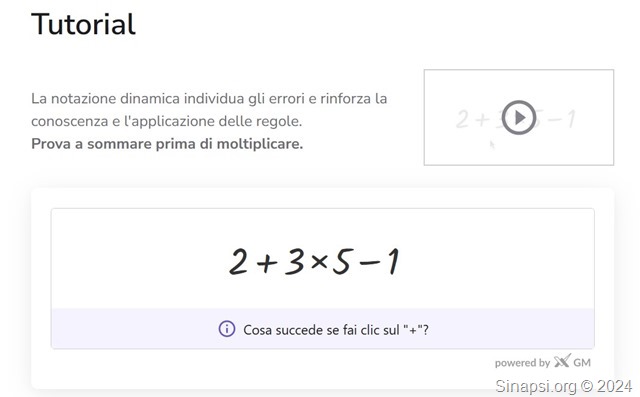
Ottieni supporto mirato nello svolgimento passo a passo di esercizi interattivi, per esplorare percorsi risolutivi diversi e acquisire sicurezza nella soluzione dei problemi algebrici.
La collega srmathmum ha preparato alcuni video che illustrano molto bene tutte le nuove bellissime funzioni appena aggiunte e disponibili anche in italiano.



