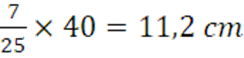Archivi tag: problema

Conosco l’area del trapezio rettangolo

Lascia una risposta

Un nostro lettore di seconda media ci ha chiesto aiuto per risolvere questo problema di geometria.

Problema: Un trapezio rettangolo ha l’area di 2400 cm² e l’altezza di 30 cm. Sapendo che la base maggiore è i 5/3 della minore, calcola il perimetro.

Soluzione: Conoscendo area e altezza possiamo utilizzare la formula inversa:

clip_image002

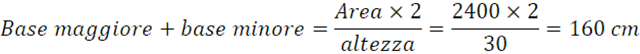
Poi applichiamo la proprietà del comporre alla proporzione:

Da cui ricaviamo la Base maggiore 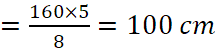clip_image006

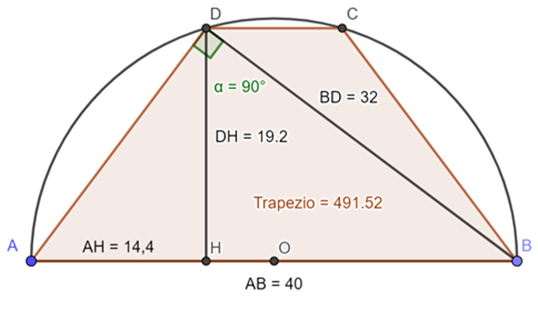
per cui la base minore . Adesso possiamo disegnare la figura per capire come calcolare il lato obliquo.

clip_image010

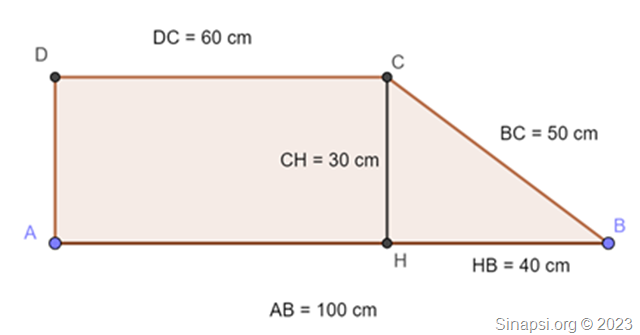
Usiamo il teorema di Pitagora per calcolare

Infine il perimetro

Trapezio isoscele inscritto in una semicirconferenza

Lascia una risposta

Una nostra lettrice ci manda questo problema di geometria.

In una semicirconferenza avente il raggio di 20 cm è inscritto un trapezio isoscele. Il lato obliquo del trapezio misura 24 cm e la base minore è 7/25 della maggiore. Calcola la misura della diagonale e l’area del trapezio.

Vediamo come si risolve.

La base maggiore del trapezio inscritto nella semicirconferenza misura come il diametro: 40 cm.

La base minore è clip_image002

Questa è la figura:

clip_image004

Con Pitagora troviamo l’altezza del trapezio:

Area del trapezio:

Diagonale del trapezio:

Ricordate che se anche voi volete un suggerimento potete inviare il vostro problema seguendo le istruzioni che trovate qui: https://www.sinapsi.org/wordpress/tutorial/vuoi-un-aiuto/