Dopo aver ripassato i concetti principali relativi alle potenze, possiamo provare a ridurre questa espressione.

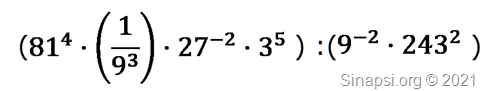
Dopo aver notato che tutte le basi (81; 9; 27 e 243) sono multiple di 3, possiamo ridurre tutte le potenze alla stessa base:

81⁴=(3⁴)⁴=3^4·4=3¹⁶ ;  9³=(3²)³=3^2·3=3⁶  ;  27^-2=(3³)^-2=3^3·(-2)=3^-6  ;   9^-2=(3²)^-2=3^2·(-2)=3^-4  ;  243²=(3⁵)²=3^5·2=3¹⁰

Quindi l’espressione diventa:

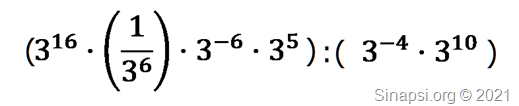
Ricordando che se si inverte la base allora l’esponente cambia di segno:

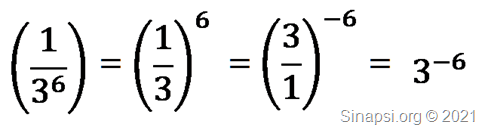
Abbiamo:

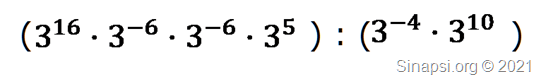
Ricordiamo che dal prodotto di potenze con base uguale si ottiene una potenza con la stessa base e con esponente uguale alla somma algebrica degli esponenti.

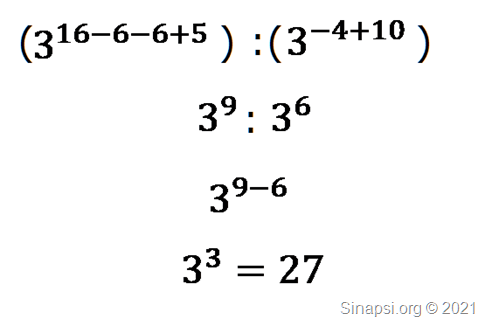
Vediamo infine se abbiamo compreso a fondo questi passaggi risolvendo questa espressione che si semplifica riducendo le potenze alla stessa base:

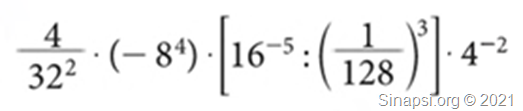
Notiamo che le basi sono multiple di 2, infatti abbiamo che: 2²=4;  2³=8;  2⁴=16;  2⁵=32; 2⁶=64;  2⁷=128.