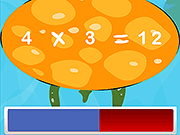“Turtle Math” è una sfida aritmetica dal ritmo frenetico in cui la rapidità di pensiero e le capacità di calcolo sono fondamentali. I giocatori devono risolvere problemi aritmetici prima che scada il tempo, accelerando il ritmo man mano che il gioco procede. Con un flusso infinito di problemi di matematica, la sfida si intensifica nel tempo, mantenendo i giocatori impegnati e all’erta. Metti alla prova la tua agilità mentale e la tua abilità aritmetica in questa emozionante e infinita avventura matematica!
Archivi categoria: Matematica
Può un gioco cambiare la tua percezione della matematica?
L’istituto di ricerca MIND pensa che sia possibile.

MIND Education coinvolge, motiva e sfida gli studenti verso il successo in matematica. È il creatore di ST Math, un programma didattico visivo PreK-8 che sfrutta l’innata capacità di ragionamento spazio-temporale del cervello per risolvere problemi matematici, e InsightMath, un programma di studio K-6 basato sulle neuroscienze che trasforma l’apprendimento degli studenti insegnando la matematica nel modo in cui il cervello impara in modo che tutti gli studenti siano attrezzati per avere successo.
Ma cos’è ST Math?
È un programma didattico visivo che sfrutta l’innata capacità di ragionamento spazio-temporale del cervello per risolvere problemi matematici.
L’approccio unico e brevettato di ST Math offre agli studenti un accesso equo all’apprendimento attraverso enigmi stimolanti, risoluzione di problemi non di routine e feedback formativo.
Con ST Math, gli studenti sviluppano una profonda comprensione concettuale e le scuole vedono risultati comprovati e ripetibili.
Attualmente ST Math è disponibile solo per le scuole degli USA, Canada, Nuova Zelanda e Australia però è possibile utilizzarlo gratuitamente come home schooling con la sola limitazione che si possono seguire al massimo 10 studenti.
Il bello di questi giochi interattivi è che non hanno istruzioni! Ma allora come si gioca? Semplicemente provando e riprovando fintanto che JiJi (il pinguino mascotte) sarà soddisfatto del vostro risultato. Il vantaggio di questo approccio senza istruzioni verbali è quello di essere comprensibile al di là delle barriere linguistiche.
Se volete provare questo gioco, cliccate qui. JiJi è un pinguino alto 90 cm in viaggio nel mondo di ST Math. Gli studenti aiutano JiJi a superare gli ostacoli risolvendo enigmi matematici e associano JiJi al brivido della sfida e del successo. JiJi attraversa lo schermo ogni volta che uno studente completa con successo un puzzle, conducendolo alla sfida successiva. JiJi è curioso, tenace, paziente e amichevole.
Il nome JiJi significa “piccolo pollo” in mandarino.
Volete iniziare ad usare ST Math? Ecco come fare: