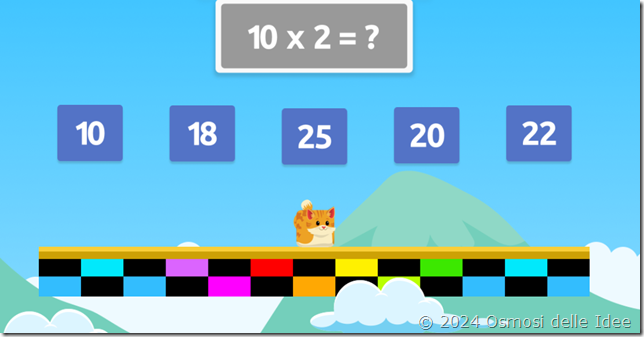
Introduzione al gioco Sticky Tables
Sticky Tables è un gioco didattico divertente e coinvolgente pensato per alunni di circa 12 anni. Questo gioco unisce abilità motorie e apprendimento della matematica, in particolare le tabelline. È perfetto per allenare i riflessi e ripassare i calcoli in modo originale e dinamico.
Come giocare a Sticky Tables
In Sticky Tables, impersoni un simpatico personaggio di slime appiccicoso che può muoversi solo saltando. Per saltare, basta premere un pulsante: più lo tieni premuto, più alto sarà il salto. Il tuo obiettivo è superare gli ostacoli presenti nei vari livelli e raggiungere la fine del percorso.
Ma non è solo un gioco di abilità! Alla fine di ogni livello, ti verranno poste delle domande sulle tabelline. Rispondendo correttamente, guadagnerai stelle: 3 stelle se rispondi a tutte le domande senza errori. Se sbagli, dovrai ripetere il livello. Puoi scegliere quali tabelline esercitare, da 1 a 12, e cambiarle in qualsiasi momento, anche durante il gioco.
Ricompense e personalizzazioni
Avanzando nei livelli, guadagnerai monete da spendere nel negozio per personalizzare il tuo slime con skin uniche e divertenti: leone, gecko, panda o persino un drago. Sono disponibili anche skin a tema festivo, come Babbo Natale o una zucca spaventosa. Hai bisogno di più monete? Risolvi altre domande sulle tabelline per ottenerle! Se trovi un livello troppo difficile, puoi risolvere un quiz per saltarlo.
Comandi di gioco
Il personaggio salta caricando l’altezza del salto con precisione:
- Carica il salto: Tieni premuto il pulsante sinistro del mouse o il dito sullo schermo (versione mobile).
Un modo nuovo di imparare le tabelline
Sticky Tables ti aiuta a memorizzare le tabelline in modo divertente, senza bisogno di un abbonamento. È un ottimo strumento per migliorare le abilità matematiche nella scuola primaria e divertirsi allo stesso tempo!
Preparati a saltare, schivare e imparare con Sticky Tables!