Quando una retta taglia due parallele, si formano queste coppie di angoli.
Angoli alterni (sono dalle parti opposte della retta che taglia) interni (sono dentro alle parallele) sono congruenti:

Angoli alterni (sono dalle parti opposte della retta che taglia) esterni (sono fuori delle parallele) sono congruenti:

Angoli coniugati (sono dalla stessa parte della retta che taglia) interni (sono dentro alle parallele) sono supplementari (la loro somma è una angolo piatto di 180°):

Angoli coniugati (sono dalla stessa parte della retta che taglia) esterni (sono fuori delle parallele) sono supplementari (la loro somma è una angolo piatto di 180°):

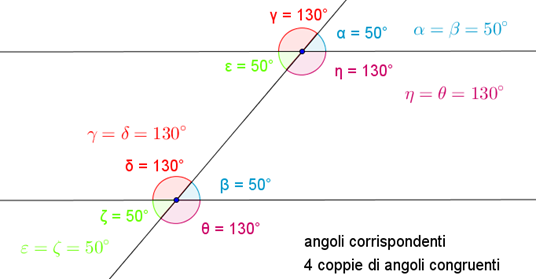
Angoli corrispondenti (dalla stessa parte sia della retta che taglia che delle parallele) sono 4 coppie di angoli congruenti:
Con il seguente strumento interattivo potete visualizzare una semplice animazione relativa agli angoli alterni. Prima di iniziare clicca sul pulsante Reset.