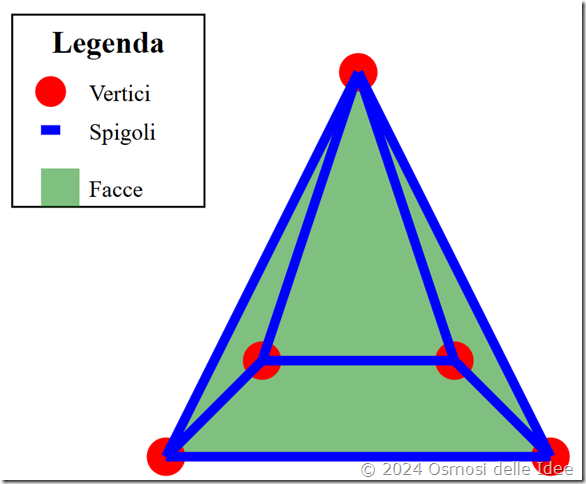
Cosa sono le proiezioni ortogonali e a cosa servono?

Immagina di voler disegnare l’ombra di un oggetto su un muro. L’ombra è un’immagine semplice che rappresenta l’oggetto da un punto di vista particolare. In matematica e geometria, quando vogliamo rappresentare qualcosa in modo semplice e chiaro, usiamo un concetto simile chiamato proiezione ortogonale.

Che cos’è una proiezione ortogonale?
La proiezione ortogonale è come l’ombra di un oggetto, ma invece di usare la luce, si usa una linea perpendicolare (cioè una linea che forma un angolo di 90 gradi) rispetto alla superficie su cui stiamo proiettando. L’oggetto può essere una figura nello spazio tridimensionale (3D), e la superficie su cui lo proiettiamo è come una “fotografia” bidimensionale (2D).

Un esempio semplice: immagina di avere un foglio di carta e di mettere sopra un cubo. Se guardi il cubo dall’alto, ciò che vedresti proiettato sul foglio sarebbe un quadrato, che è l’ombra del cubo. Questa “ombra” si chiama proiezione ortogonale.

Come si fa una proiezione ortogonale?
Per capire meglio, prova a pensare a questi tre passi:
1. Oggetto nello spazio: Hai un oggetto, ad esempio un punto, una linea o una figura geometrica nello spazio tridimensionale.
2. Superficie di proiezione: C’è un piano (come un foglio) su cui vuoi proiettare l’oggetto.
3. Linea perpendicolare: Disegni delle linee immaginarie perpendicolari al piano, che partono da ogni punto dell’oggetto e arrivano sulla superficie. Il punto in cui queste linee toccano la superficie è la proiezione ortogonale.

A cosa servono?
Le proiezioni ortogonali sono molto utili in geometria, nell’arte e in altre discipline, come l’architettura e l’ingegneria. Ecco alcuni esempi pratici:

Geometria: Quando studiamo figure geometriche in tre dimensioni, le proiezioni ortogonali ci aiutano a capire meglio come appaiono su un piano. Ad esempio, per risolvere alcuni problemi di matematica, proiettare una figura 3D su un piano ci permette di analizzarla più facilmente.
Disegno tecnico: Gli ingegneri e gli architetti usano le proiezioni ortogonali per creare disegni precisi di edifici o macchinari. Grazie a queste proiezioni, possono vedere l’oggetto da diverse angolazioni (dall’alto, di fronte, di lato) e progettare le strutture con precisione.
Arte e prospettiva: Anche gli artisti, quando disegnano oggetti in prospettiva, usano concetti simili per rappresentare la realtà su un foglio bidimensionale.

Un esempio semplice
Immagina di avere una scatola (un cubo) su un tavolo e di voler vedere come appare su una parete di fronte a te. Le proiezioni ortogonali ti mostrerebbero questa scatola come un rettangolo visto di fronte, un quadrato dall’alto e un altro rettangolo di lato. Questi tre disegni ci danno tutte le informazioni necessarie per capire la forma e le dimensioni della scatola.

Conclusione
Le proiezioni ortogonali sono uno strumento che ci aiuta a semplificare e comprendere meglio gli oggetti nello spazio. Ci permettono di rappresentare oggetti tridimensionali in modo chiaro su superfici bidimensionali, il che è fondamentale sia in geometria che nella vita quotidiana.

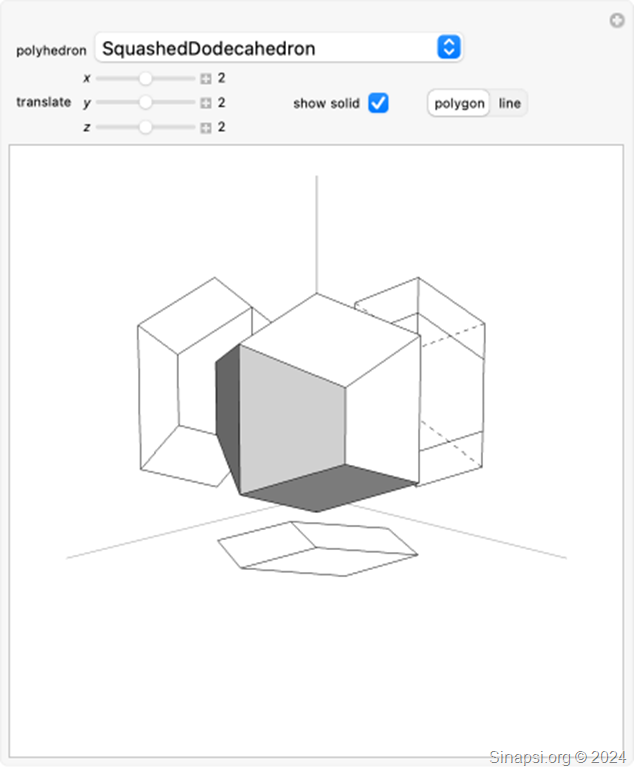
Ora che hai capito cosa sono e a cosa servono, prova ad interagire con questa serie di solidi usando il tuo mouse per vedere come vengono proiettate le loro immagini sui piani orizzontale e verticali. Seleziona dal menù a discesa uno dei tanti solidi elencati: Cubo, Dodecaedro, Piramide e tanti altri.

Schermo intero