Problema di geometria per studente di 12 anni

Lascia una risposta

Oggi non sapevo bene cosa inventarmi e allora ho chiesto all’Intelligenza Artificiale.

Inventa un problema di geometria adatto ad uno studente di 12 anni

Ed ecco cosa mi ha proposto:

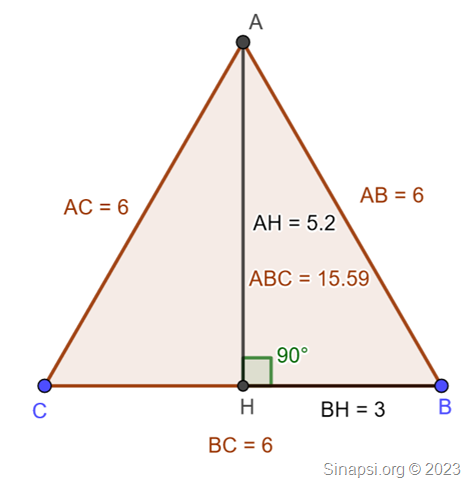
Immagina di avere un triangolo equilatero ABC con lato di lunghezza 6 cm. Disegna la sua altezza AH, che parte dall’angolo A e arriva sul lato BC.

Qual è la lunghezza dell’altezza AH? E qual è l’area del triangolo ABC?

A questo punto volevamo vedere se la sua spiegazione era abbastanza convincente:

Bene, adesso dammi la soluzione completa di questo problema.

triango

Certamente, ecco la soluzione completa al problema di geometria che ho proposto:

Il lato del triangolo equilatero ABC ha lunghezza 6 cm. La lunghezza dell’altezza AH può essere calcolata utilizzando il teorema di Pitagora. Sia h la lunghezza dell’altezza AH, b la lunghezza del segmento BC e a la lunghezza del segmento AB. Poiché il triangolo è equilatero, si ha a=b=6 cm. Applicando il teorema di Pitagora al triangolo rettangolo ABH, si ha:

h^2 = a^2 - \left(\frac{a}{2}\right)^2 = 6^2 - \left(\frac{6}{2}\right)^2 = 36 - 9 = 27

Quindi la lunghezza dell’altezza AH è:

h = \sqrt{27} = 3\sqrt{3} \approx 5.196\text{ cm}

L’area del triangolo ABC può essere calcolata utilizzando la formula dell’area del triangolo, che è data da:

A=\frac{1}{2}(6)(5.196) \approx 15.588 \text{ cm}^2

Quindi l’area del triangolo ABC è di circa A \approx 15.588\text{ cm}^2.

Ogni commento è molto gradito, scrivici!