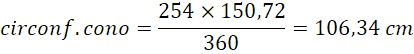Un nostro visitatore ci ha proposto questo problema:
Determinare il volume di un cono la cui superficie laterale si sviluppa in un settore circolare di 254° e raggio 24 cm.
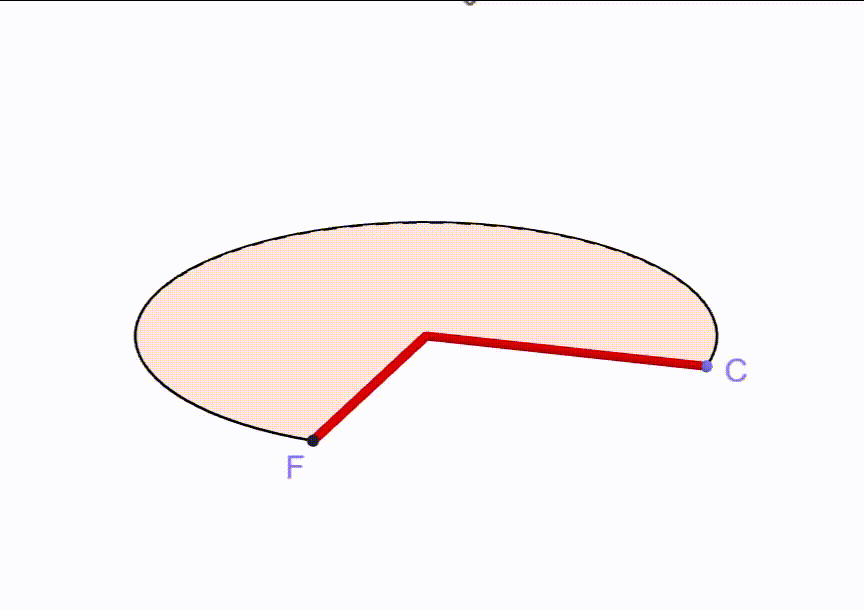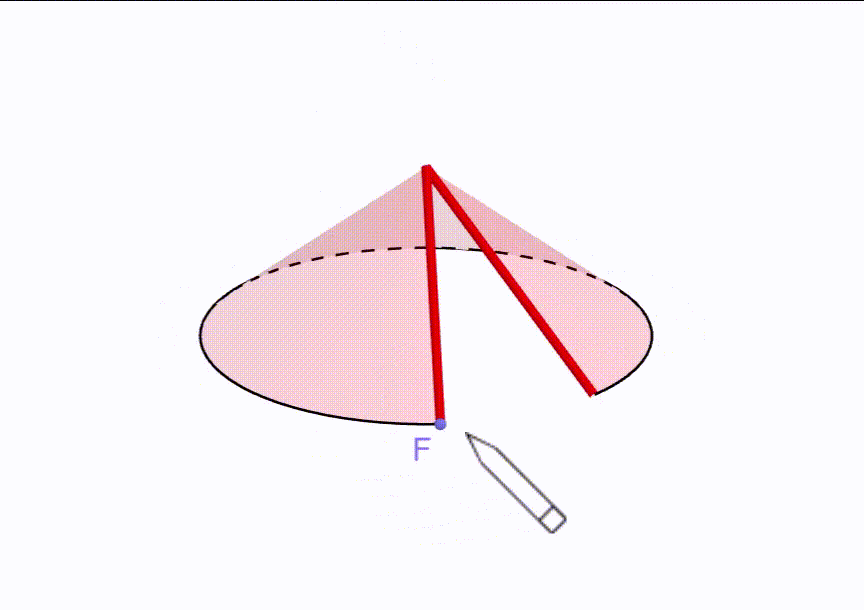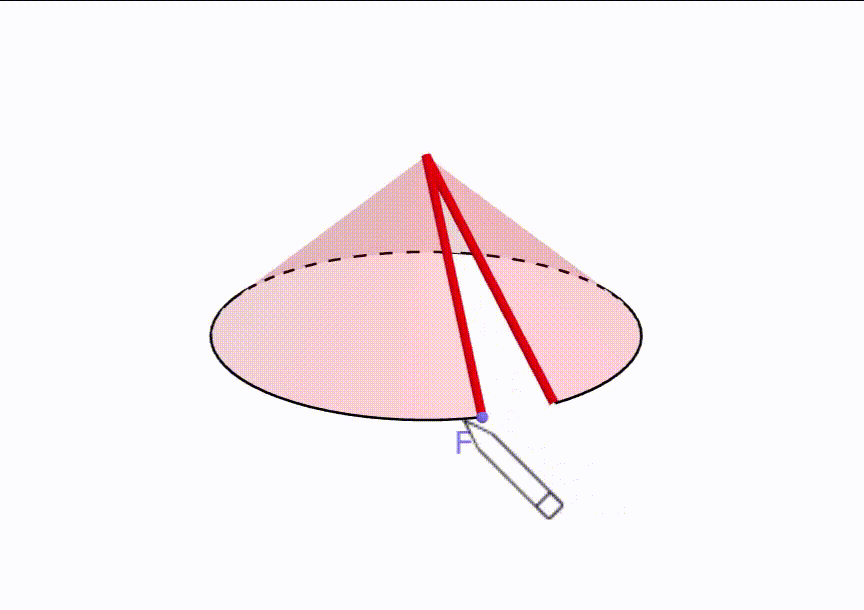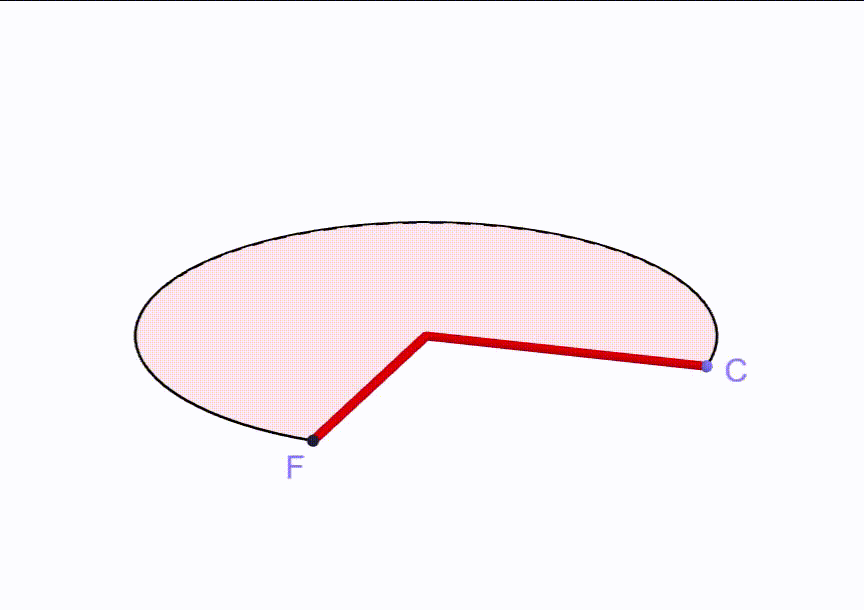
Per capire come risolvere questo quesito conviene guardare cosa significa ottenere un cono a partire da un settore circolare.
Vediamo che la linea rossa (raggio del settore = 24 cm) diventa l’apotema del cono.
Inoltre si capisce che l’arco di circonferenza (quello che unisce F con C) diventa la circonferenza della base del cono.
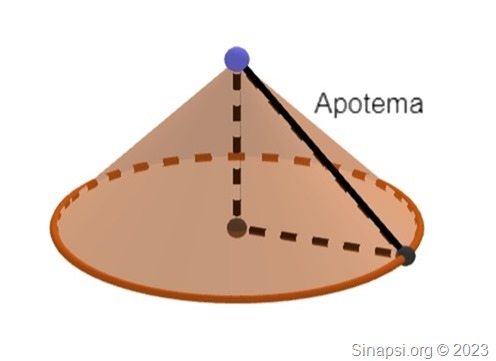
Soluzione: Il raggio del settore circolare è l’apotema del cono. Quando chiudi il settore circolare ottieni il cono quindi la sua circonferenza la ricavi da questa proporzione:
254° : circonferenza del cono = 360° : circonferenza totale del settore
La circonferenza totale del settore è 
Risolvo la proporzione: 
Adesso calcolo il raggio di base del cono: 
Per trovare il volume ci serve l’altezza 
