Più di un matematico ha ricevuto una lunga lettera da un mittente sconosciuto che sostiene di avere trovato un modo per trisecare un angolo usando solo riga e compasso.
Il matematico leggerà la lettera ad alta voce ai colleghi, sorseggiando il tè del pomeriggio. Senza bisogno di analizzare i dettagli, il matematico saprà bene che la conclusione della lettera non può essere corretta.
Infatti, nel XIX secolo, il giovane matematico francese Evariste Galois dimostrò come il problema sia impossibile da risolvere.
(La geometria euclidea si basa su un insieme di assiomi usati per creare figure e dimostrare teoremi. Tali assiomi permettono di creare linee rette collegando due punti o estendendo una linea esistente. Inoltre, permettono di creare circonferenze a partire da segmenti di lunghezza data. Le linee di Euclide sono astrazioni matematiche che possono essere rappresentate in un disegno o un diagramma. Creare questi disegni o diagrammi comporta l’utilizzo di due soli strumenti: una riga e un compasso.)
Più recentemente, i matematici hanno scoperto che è possibile dividere un angolo in tre parti uguali piegando un quadrato di carta, senza usare riga e compasso.
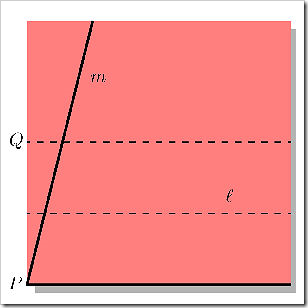
Il primo passo per la trisezione di un angolo è quello di mettere un lato dell’angolo lungo il bordo inferiore del quadrato di carta.
Il passo successivo è quello di aggiungere due linee parallele al bordo inferiore, in modo che le linee superiori ed inferiori siano equidistanti da quella centrale. P è il punto in basso a sinistra, Q è il punto dove la linea superiore incontra il lato verticale sinistro del quadrato.
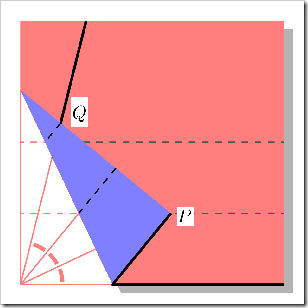
Infine si piega la carta in modo da far cadere i punti P e Q rispettivamente sulle linee “l” e “m”.
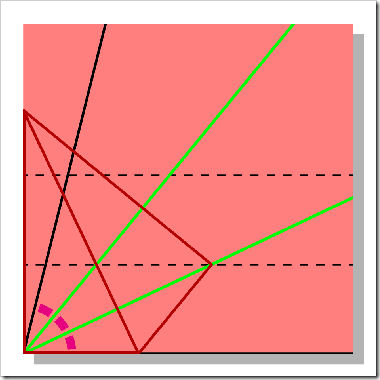
Riaprendo il foglio di carta, vediamo come le linee verdi trisechino l’angolo originale. Le linee rosse indicano dove la carta è stata ripiegata.
Da notare come il teorema di Galois rimanga valido: trisecare un angolo usando solo riga e compasso è impossibile.
Per verificare questa bella proprietà dell’Origami potete prendere un vero pezzo di carta oppure giocare con questo applet di GeoGebra.
Spostate il punto “D” per modificare l’angolo da trisecare, poi muovete i punti “J” e “K” per far coincidere ” H’ ” sul lato superiore dell’angolo e ” A’ ” sulla retta orizzontale passante da “F”.
Vedrete che l’angolo sarà diviso in tre parti uguali (salvo approssimazioni).
Bill Casselman della University of British Columbia di Vancouver, spiega questa tecnica nel numero di maggio del 2007 di Notices of the American Mathematical Society
Il suo articolo è basato su Project Origami: Activities for Exploring Mathematics (2006, A.K. Peters Ltd.).