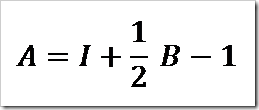Il geopiano è una tavoletta ricoperta da un reticolo regolare di piccoli pioli attorno ai quali si possono agganciare elastici per formare poligoni o segmenti.
Venne inventato, verso il 1950, da Caleb Gattegno (1911-1988), scienziato, matematico, pedagogista egiziano.
Il suo utilizzo consente un approccio manuale ai concetti di perimetro, area, lunghezza, estensione e trasformazioni nel piano.
Un’interessante teorema consente il calcolo dell’area contenuta in un poligono costruito sul geopiano (poligono reticolare).
dove A=area; B=numero di pioli lungo il perimetro; I=numero di pioli all’interno del poligono.
(L’area ottenuta ha come unità di misura la distanza tra un piolo e l’altro, al quadrato)
Applichiamo il teorema a questi due triangoli.
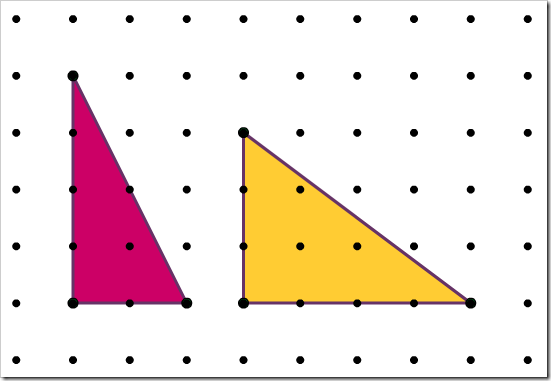 Quello rosa ha B=8 pioli lungo il perimetro e I=1 solo piolo al suo interno, quindi la sua area sarà:
Quello rosa ha B=8 pioli lungo il perimetro e I=1 solo piolo al suo interno, quindi la sua area sarà:
A=1+8/2-1=4 unità quadrate.
Quello giallo ha B=8 pioli lungo il perimetro e I=3 pioli all’interno, quindi avremo che
A=3+8/2-1=6 unità quadrate.
Il teorema di Pick risulta particolarmente utile nel caso di poligoni reticolari irregolari, come questo:
 Area=9+10/2-1=13 unità quadrate.
Area=9+10/2-1=13 unità quadrate.
Infine provate voi stessi con questo Geopiano virtuale