Archivi tag: numeri primi

Visualizza la fattorizzazione in numeri primi

Lascia una risposta

I numeri primi sono interi, maggiori di 1, che si possono dividere soltanto per 1 e per sé stessi.

Un numero intero che non è primo si dice composto.

Scomporre un numero intero in fattori primi significa trovare la serie di numeri primi che, moltiplicati tra loro, danno come risultato il numero intero di partenza.

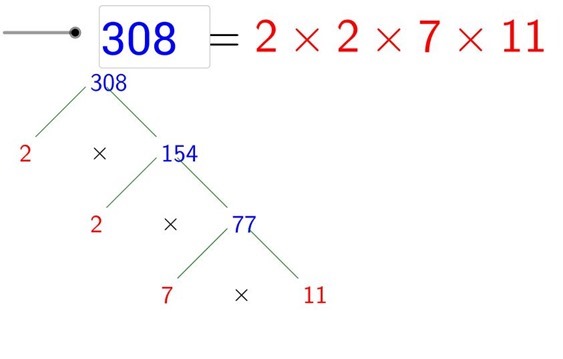
Ad esempio il numero composto 308 si ottiene moltiplicando tra loro 2 x 2 x 7 x 11 e questa fattorizzazione si scrive:

308 = 22 x 7 x 11

fattori

Nel nostro sito abbiamo raccolto molti strumenti interattivi dedicati a questo argomento, oggi ne aggiungiamo uno nuovo, realizzato con GeoGebra, che visualizza in un grafo il procedere della fattorizzazione.

Una volta scritto il numero da scomporre nella casella in alto a sinistra basta pigiare il tasto “Invio” per vedere la scomposizione procedere a cascata come nell’immagine qui sopra.

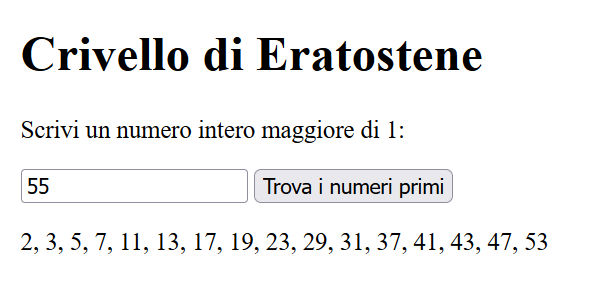
Infine un interattivo scritto con l’aiuto di ChatGPT:

Crivello di Eratostene

Lascia una risposta

Il Crivello di Eratostene è un algoritmo antico e semplice che viene utilizzato per trovare tutti i numeri primi fino a un determinato numero intero.

Crivello di Eratostene

Ecco i passaggi concettuali che spiegano il funzionamento del Crivello di Eratostene:

  1. Creazione di una lista di numeri da 2 a n: Per utilizzare il Crivello di Eratostene, prima di tutto dobbiamo creare una lista di numeri da 2 a n, dove n è il numero fino a cui vogliamo trovare i numeri primi.
  2. Iniziare dal primo numero primo: Iniziamo dal primo numero primo della lista, ovvero 2.
  3. Eliminazione dei multipli di 2: Considerando 2 come il primo numero primo, eliminiamo tutti i suoi multipli dalla lista. Ad esempio, 4, 6, 8, 10, ecc. sono tutti multipli di 2 e quindi vengono eliminati dalla lista.
  4. Passare al successivo numero primo: Passiamo al successivo numero primo nella lista, ovvero 3. In questo caso, eliminiamo tutti i multipli di 3 dalla lista, ad esempio 6, 9, 12, ecc.
  5. Continuare fino a raggiungere la fine della lista: Procediamo in questo modo finché non abbiamo eliminato tutti i multipli di tutti i numeri primi nella lista fino a raggiungere il valore n.
  6. I numeri rimasti sono i numeri primi: Alla fine del processo, tutti i numeri rimasti nella lista sono i numeri primi che stavamo cercando.
  7. Output della lista dei numeri primi: Alla fine del processo, è possibile ottenere l’elenco dei numeri primi trovati.

Il Crivello di Eratostene è un algoritmo efficiente per trovare i numeri primi, ma la sua efficacia dipende dalla dimensione della lista di numeri. In generale, è più veloce di altri algoritmi di ricerca dei numeri primi per elenchi di numeri relativamente piccoli.

Naturalmente questo procedimento può essere svolto anche da un algoritmo come questo scritto in JavaScript:

<script> function sieve() { let n = parseInt(document.getElementById("input").value); let primes = []; let isPrime = new Array(n+1).fill(true); for (let i = 2; i*i <= n; i++) { if (isPrime[i]) { for (let j = i*i; j <= n; j += i) { isPrime[j] = false; } } } for (let i = 2; i <= n; i++) { if (isPrime[i]) { primes.push(i); } } document.getElementById("output").innerHTML = primes.join(", "); } </script>

Abbiamo utilizzato le righe di codice per ottenere questo strumento che ci fornirà istantaneamente tutti i numeri primi minori di quello che abbiamo inserito.