Generi di leve
Un martello può essere usato per estrarre un chiodo da una tavola. Puoi vedere come è fatto in questa immagine. Quando si spinge verso il basso il manico del martello, l’estremità dell’artiglio del martello tira verso l’alto il chiodo. Un martello è un esempio di macchina chiamata leva.

Altre leve cambiano la forza o la distanza in modi diversi rispetto a un martello che rimuove un chiodo. Il modo in cui una leva cambia forza o distanza dipende dalla posizione delle forze di ingresso e di uscita rispetto al fulcro. La forza di ingresso è la forza applicata dall’utente alla leva. La forza di uscita è la forza applicata dalla leva all’oggetto. In base alla posizione delle forze di ingresso e di uscita, esistono tre tipi fondamentali di leve, chiamate leve di primo genere, di secondo genere e di terzo genere. La tabella seguente descrive i tre generi.
|
Generi di leve |
||||
|
Genere di leva |
Esempio di leva in questa Genere |
Posizione delle forze di ingresso e di uscita e del fulcro* |
Vantaggio meccanico ideale |
Cambio di direzione della forza? |
|
Primo Genere |
Altalena
|
|
1 < 1 > 1 |
Sì Sì Sì |
|
Secondo Genere |
Carriola
|
|
> 1 |
No |
|
Terzo Genere |
Mazza da hockey
|
|
< 1 |
No |
- Δ = fulcro I = forza di ingresso O = forza di uscita
La tabella sopra include il vantaggio meccanico ideale di ciascun genere di leva. Il vantaggio meccanico è il fattore in base al quale una macchina modifica la forza di input. Il vantaggio meccanico ideale è l’aumento o la diminuzione della forza che si verificherebbe se non ci fossero attriti da superare nell’uso della macchina. Poiché tutte le macchine devono superare un certo attrito, il vantaggio meccanico ideale è sempre un po’ maggiore dell’effettivo vantaggio meccanico della macchina così come viene utilizzata nel mondo reale.
D: Che genere di leva è un martello quando viene utilizzato per estrarre un chiodo da una tavola? Qual è il suo vantaggio meccanico?
R: Per estrarre un chiodo da una tavola, il fulcro si trova tra le forze di ingresso e di uscita. Pertanto, quando un martello viene utilizzato in questo modo, è una leva di primo genere. Il fulcro è più vicino alla forza di uscita rispetto alla forza di ingresso, quindi il vantaggio meccanico è > 1. In altre parole, il martello aumenta la forza applicata, rendendo più facile fare leva sul chiodo dalla tavola.
Avvia la simulazione qui sotto per esplorare ulteriormente come funziona un’altalena come leva di primo Genere:
Potrà Sara sollevare sua mamma? Come dovrà fare? Quanto dovrà andare distante dal fulcro?

 [Figura 2]
[Figura 2]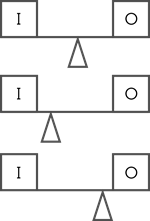 [Figura 3]
[Figura 3] [Figura 4]
[Figura 4]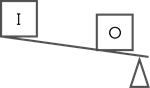 [Figura 5]
[Figura 5] [Figura 6]
[Figura 6] [Figura 7]
[Figura 7]