Come si risolve un problema di geometria

Lascia una risposta

Il nostro sito ha ricevuto, nel corso degli anni, moltissime richieste di aiuto nel risolvere problemi di geometria.

Per prima cosa consigliamo di consultare la nostra pagina che permette di ripassare ed utilizzare le formule necessarie a risolvere i più comuni problemi di geometria solida e piana.

Se poi qualcuno volesse un aiuto più approfondito e completo potrà inserire la sua richiesta nella pagina “Vuoi un aiuto?”.

In poco tempo riceverà il problema risolto con tutti i passaggi ed i disegni relativi.

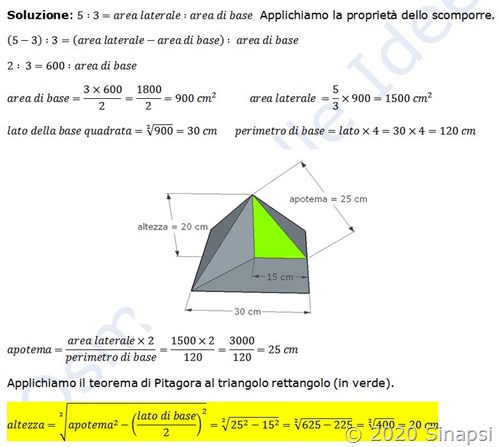
Come esempio vi mostriamo la soluzione di questo problema di terza media:

In una piramide quadrangolare regolare l’area di base è i 3/5 dell’area laterale e la loro differenza è di 600 cm. Calcola l’altezza della piramide

Soluzione:

20150208a

Area del parallelogramma

Lascia una risposta

Dimostrazione senza parole.

In matematica, una dimostrazione senza parole è una prova di un’identità o di una dichiarazione matematica che può essere dimostrata come evidente da un diagramma senza alcun testo esplicativo di accompagnamento.

Tali prove possono essere considerate più eleganti di quelle formali o matematicamente rigorose a causa della loro natura evidente.

Quando il diagramma dimostra un caso particolare di una dichiarazione generale, per essere una prova, deve essere generalizzabile.

Gli studenti delle medie inferiori possono accedere a questo tipo di dimostrazioni utilizzando il potente e gratuito software Geogebra.

Come esempio mostriamo il calcolo dell’area del parallelogramma.

parallelogramma

Aspettate che si carichi completamente la figura qui sotto prima di interagire con essa.

  1. Scegliete l’inclinazione del parallelogramma spostando il pallino rosso
  2. Cliccate sulla casella “Scomponi Parallelogramma”
  3. Fate scorrere il pallino blu verso destra per spostare i triangoli colorati dentro al parallelogramma
  4. Cliccate prima su “Conclusione” e poi su “Risposta” per vedere il risultato

Se preferite visualizzare la costruzione interattiva a pagina intera, cliccate qui.