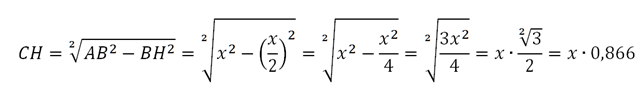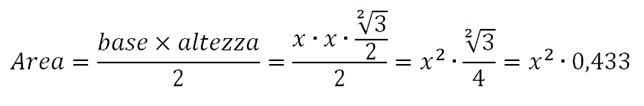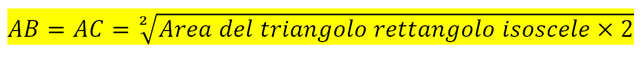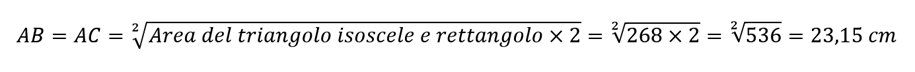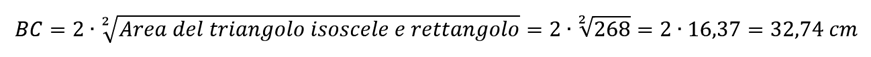Questa domanda ricorre frequentemente nei siti di domande e risposte.
Abbiamo visto che le risposte date dai tanti volonterosi utenti sono a volte confuse e poco chiare.
La risposta più frequente è: “impossibile”. Ma non è esatta, almeno non del tutto. Infatti sarebbe meglio rispondere: “dipende dal tipo di triangolo”.
Infatti ci sono alcuni casi particolari in cui è possibile trovare la lunghezza dei lati conoscendo solo l’area del triangolo, vediamoli:
Triangolo equilatero (ha i tre lati uguali)
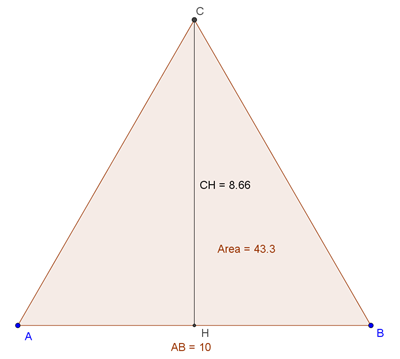
Per arrivare alla formula che ci mostra il rapporto tra area e lato del triangolo equilatero dobbiamo svolgere alcuni passaggi.
Indichiamo con x la lunghezza del lato AB e calcoliamo, con Pitagora, la lunghezza dell’altezza CH.
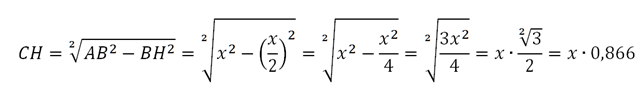
Calcoliamo adesso l’area del triangolo con la formula area = base x altezza : 2
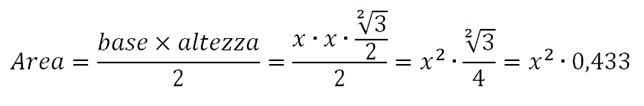
A questo punto possiamo ricavare da quest’ultima formula l’incognita “x” vale a dire il lato del triangolo equilatero.
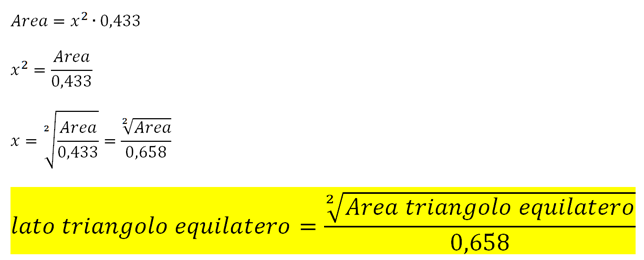
Un altro caso particolare che ci permette di trovare i lati conoscendo soltanto l’area del triangolo è quello del triangolo rettangolo isoscele.
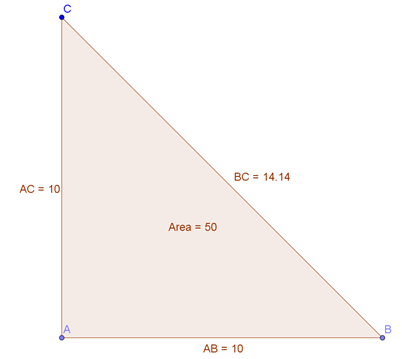
Per trovare la misura dei tre lati basta osservare che questo tipo di triangolo è la metà di un quadrato:
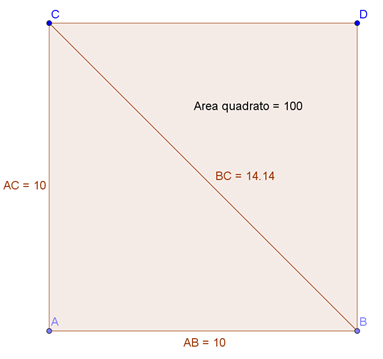
che avrà area doppia per cui i lati AB e AC (cateti uguali del triangolo rettangolo isoscele) misurano:
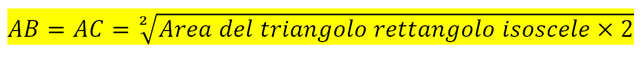
mentre il terzo lato BC (ipotenusa del triangolo rettangolo isoscele) si trova con il teorema di Pitagora:

Come vedete possiamo trovare le misure dei lati solo se si tratta di triangoli particolari, triangoli di cui conosciamo il rapporto (costante) tra base ed altezza.
Infine, come suggerito da un nostro lettore, proponiamo ulteriori esempi numerici:
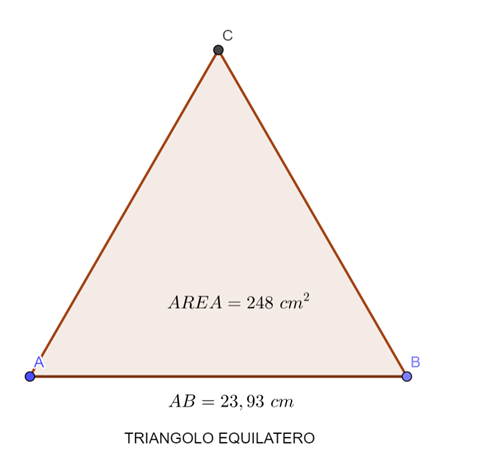
Problema N° 1: Calcolare la lunghezza del lato di un triangolo equilatero di area 248 cm2
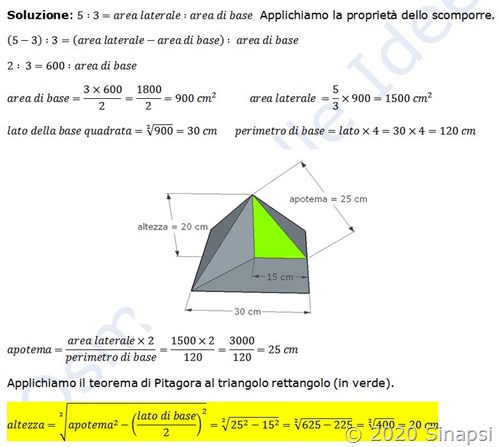
Soluzione: Applichiamo la formula che abbiamo visto nella spiegazione che precede:

Problema N°2: Calcolare la misura dei 3 lati di un triangolo isoscele e rettangolo con area di 268 cm2.
Soluzione: Anche in questo caso prendiamo la formula spiegata nelle righe precedenti.
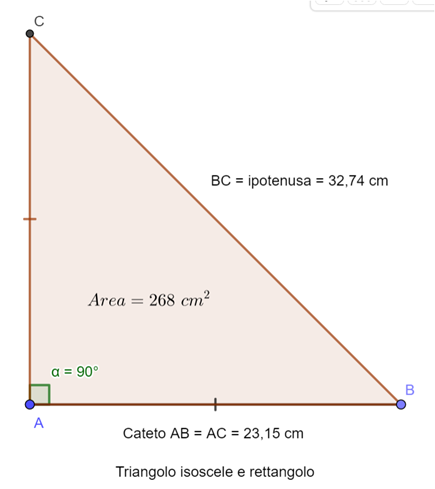
Calcoliamo prima i cateti AB e AC del triangolo isoscele e rettangolo ABC.
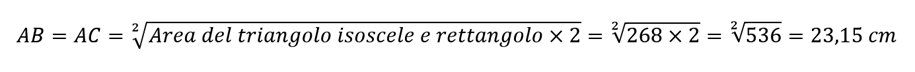
Poi troviamo l’ipotenusa BC sempre utilizzando le formule illustrate più sopra.
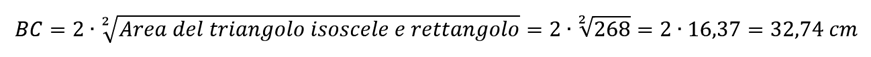
Mi piace:
Mi piace Caricamento...