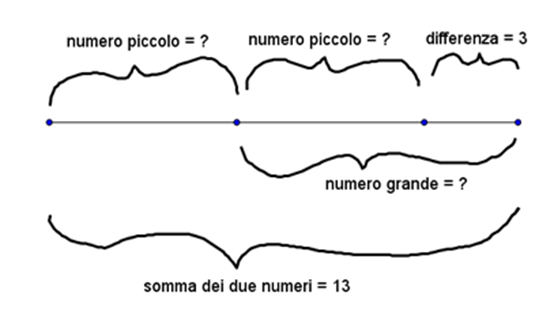
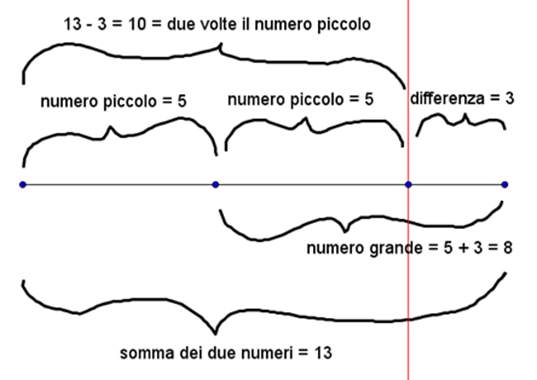
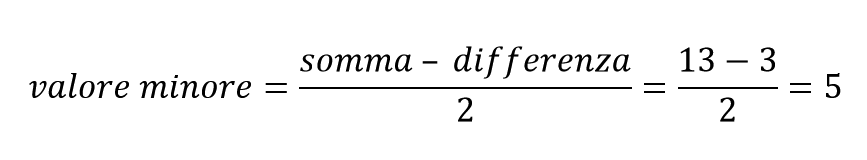Prima di iniziare bisogna ricordare come si chiamano i vari termini che formano la proporzione:

Il termine da trovare di solito si indica con la lettera “x”. Vediamo come trovare questa incognita nei vari casi:

1) la “x” è un medio:  6 : x = 3 : 5 allora il medio si trova dividendo il prodotto degli estremi per l’altro medio:

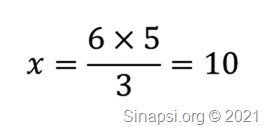
2) la “x” è un estremo: 5 : 15 = 20 : x allora l’estremo di trova dividendo il prodotto dei medi per l’altro estremo:

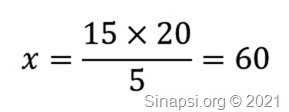
3) esiste anche il caso in cui i medi siano entrambi incognite: 12 : x = x : 27 in questo caso la proporzione di chiama “continua” e si risolve in questo modo, ricordando che la proprietà fondamentale delle proporzioni dice che il prodotto dei medi è uguale al prodotto degli estremi:

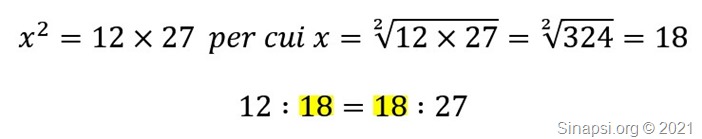
4) lo stesso vale anche nel caso in cui la proporzione continua abbia gli estremi come incognite: x : 9 = 25 : x

si usa ancora la proprietà fondamentale uguagliando il prodotto degli estremi a quello dei medi:

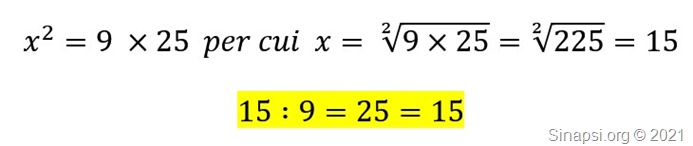
Se volete cimentarvi con alcune domande relative alle proporzioni allora cliccate qui.