Se ruoti di un angolo inferiore a 360° una figura piana attorno al suo centro e ottieni nuovamente la stessa immagine, allora si dice che quella figura ha una simmetria rotatoria.
Questa figura, ad esempio, ha una simmetria di 60°:
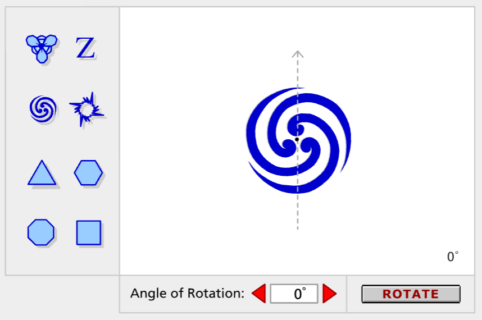
Usa il gioco interattivo per esplorare il concetto di Simmetria Rotatoria.
Clicca su Start, scegli una delle otto figure e decidi quale angolo impostare.
Clicca su Rotate per verificare la tua ipotesi.