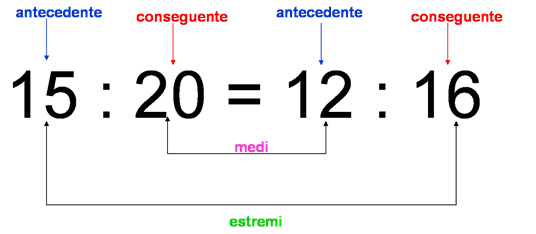
Ti sei mai chiesto come si fa a risolvere una proporzione? Una proporzione è un’uguaglianza tra due rapporti, cioè due frazioni che esprimono il rapporto tra due grandezze. Per esempio:
15 : 20 = 12 : x
Questa proporzione dice che il rapporto tra 15 e 20 è uguale al rapporto tra 12 e x. Ma come si fa a trovare il valore di x?
La soluzione è semplice: basta usare la proprietà fondamentale delle proporzioni, che dice che il prodotto degli estremi è uguale al prodotto dei mezzi. In altre parole:
15 ⋅ x = 20 ⋅ 12
Da questa equazione possiamo ricavare facilmente x dividendo entrambi i membri per 20:
x = (20 ⋅ 12) / 15
x = 16
Quindi il valore di x che rende vera la proporzione è 16.

Questo metodo si chiama anche moltiplicazione incrociata ed è molto utile per risolvere le proporzioni in modo rapido e sicuro.
Ovviamente, ci sono anche altri tipi di proporzioni che possono presentarsi, come quelle con più di un’incognita o quelle con termini frazionari. Per approfondire questi casi puoi consultare i siti web che ho trovato per te .
Spero che questo post ti sia stato utile e ti abbia fatto appassionare alle proporzioni. Le proporzioni sono uno strumento matematico molto potente e versatile, che ti permette di risolvere molti problemi pratici e teorici.
Se ti è piaciuto questo post, lascia un commento o condividilo sui tuoi social preferiti. E se hai domande o dubbi sulle proporzioni, non esitare a contattarmi. Sono sempre pronto ad aiutarti!
A presto!