Ripassiamo alcuni concetti di statistica.
La statistica è la scienza che studia fenomeni composti da singole unità sulle quali è possibile eseguire misurazioni.
Esempi:
- misurare la popolazione attualmente vivente in Italia;
- misurare le automobili circolanti in un dato periodo in Italia;
- misurare le persone diplomate in Lazio;
- misurare i litri di latte prodotti in Lombardia…
Un’indagine statistica prevede in genere almeno
tre fasi:
- Rilevazione dei dati
- Elaborazione dei dati
- Rappresentazione dei dati (con grafici, ideogrammi, istogrammi, ecc.)
La prima fase prevede la raccolta di dati che possono essere di tipo qualitativo (colore degli occhi, tipo di scuola frequentata,…) o quantitativo (età, componenti della famiglia, altezza, …). I dati possono essere raccolti su una determinata varietà di unità, detta popolazione statistica.
Dopo averli raccolti, i dati vengono elaborati:
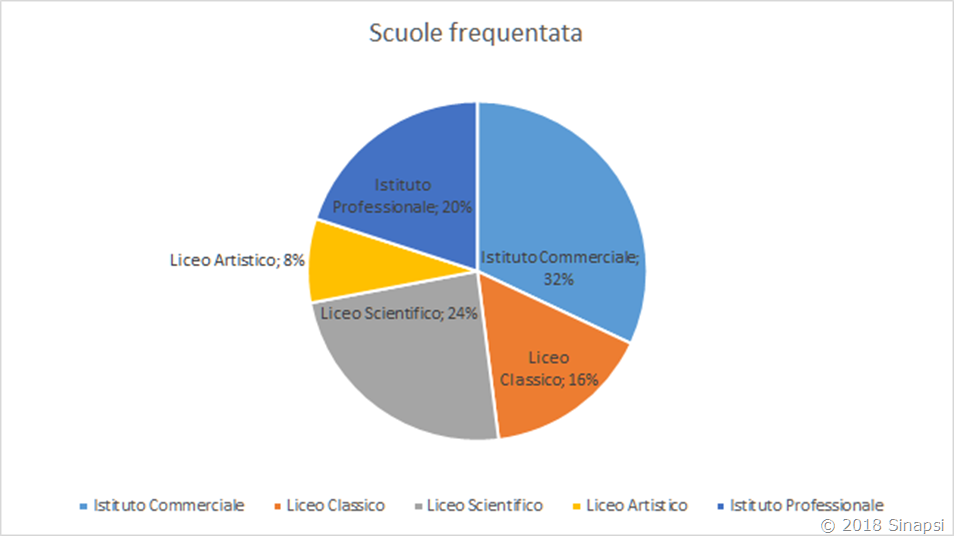
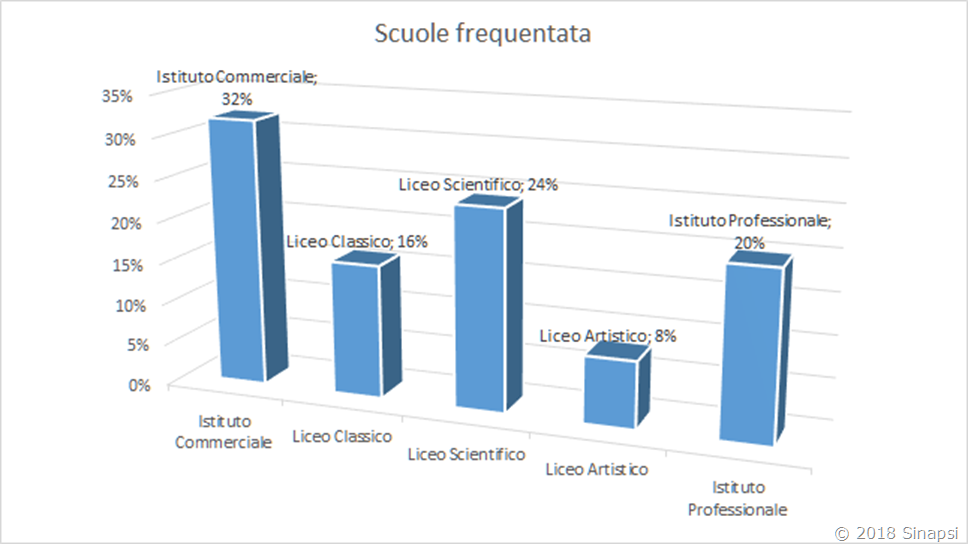
| Tipo scuola | Unità statistiche | Frequenza assoluta (f) | Frequenza relativa % |
| Istituto Commerciale | XXXXXXXX | 8 | 8/25 = 32% |
| Liceo Classico | XXXX | 4 | 4/25 = 16% |
| Liceo Scientifico | XXXXXX | 6 | 6/25 = 24% |
| Liceo Artistico | XX | 2 | 2/25 = 8% |
| Istituto Professionale | XXXXX | 5 | 5/25 = 20% |
| Totale | | 25 | |
Dopo averli elaborati vengono rappresentati graficamente in vari modi:
Grafici a torta:
Istogrammi:
Una volta raccolti e visualizzati graficamente i dati, possiamo calcolare alcuni valori significativi che ci aiutano a capirne meglio il significato.
Media Aritmetica
Si ottiene dividendo la somma dei valori di tutti i dati statistici per il loro numero.
Ad esempio se utilizziamo questa tabella che riporta i voti mensili in matematica:
| Settembre | Ottobre | Novembre | Dicembre | Gennaio | Febbraio | Marzo | Aprile | Maggio | Giugno |
| Marco | 4 | 6 | 5 | 7 | 6 | 7 | 5 | 7 | 7 | 6 |
| Lucia | 5 | 6 | 6 | 8 | 8 | 6 | 5 | 5 | 6 | 8 |
Avremo che la media di Marco sarà: (4+6+5+7+6+7+5+7+7+6)/10=60/10=6
Mentre quella di Lucia: (5+6+6+8+8+6+5+5+6+8)/10=63/10=6,3
Moda
La moda è quel valore che compare più frequentemente nella raccolta dei dati statistici.
Quindi tra i voti di Marco quello che compare con maggiore frequenza è il 7 che compare quattro volte.
La moda dei voti di Lucia invece è il 6 che figura quattro volte.
Mediana
Per calcolare la mediana di una serie di dati dobbiamo dapprima disporli in ordine crescente.
Ad esempio se abbiamo questi 11 valori:
3, 8, 10, 7, 8, 4, 9, 4, 8, 5, 4 dovremo prima di tutto trascriverli in ordine:
3, 4, 4, 4, 5, 7, 8, 8, 8, 9, 10
e adesso individuare il valore che sta in mezzo, cioè quello che segue i primi cinque e precede gli ultimi cinque
3, 4, 4, 4, 5, 7, 8, 8, 8, 9, 10
vediamo che la mediana in questo caso è 7.
Se però avessimo un numero pari di valori dovremmo fare la media tra i due valori centrali.
Come in questo caso dove ci sono dieci dati:
2, 4, 4, 5, 5, 6, 7, 7, 8, 10
in mezzo troviamo due numeri, il 5 e il 6. La mediana sarà quindi (5+6)/2=11/2=5,5
Ricordate che cliccando qui troverete anche test sulla statistica.
Mi piace:
Mi piace Caricamento...