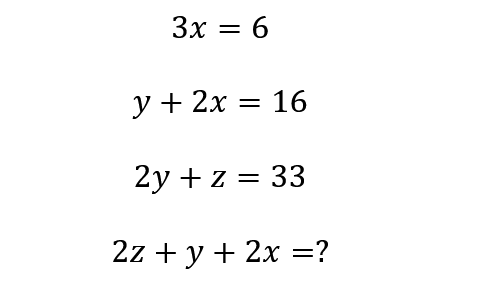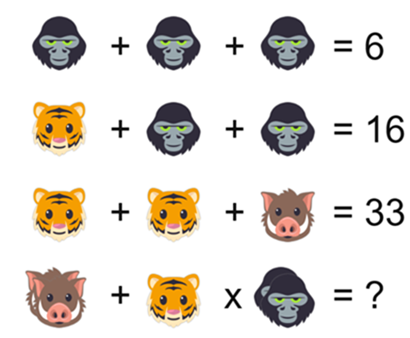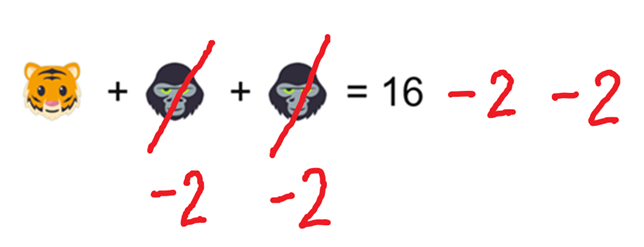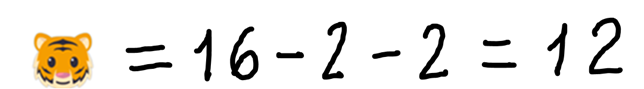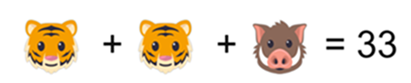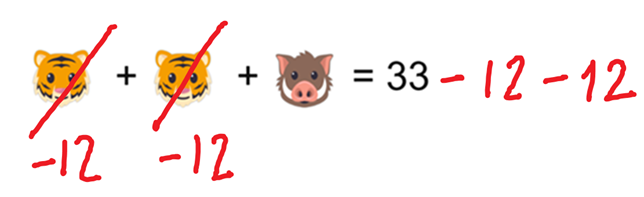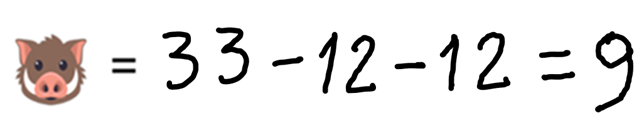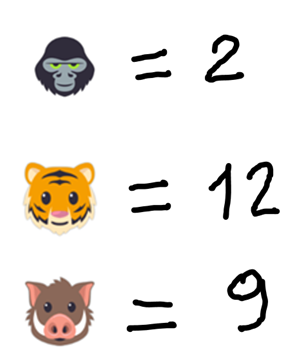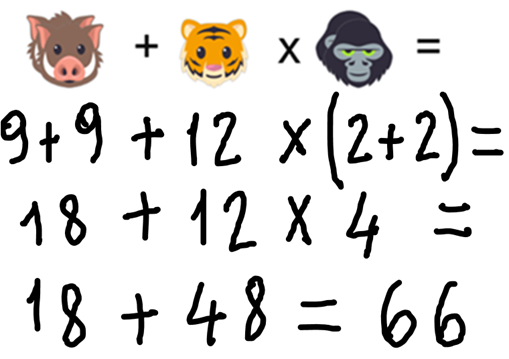L’algebra può spaventare o divertire, dipende da come viene presentata.
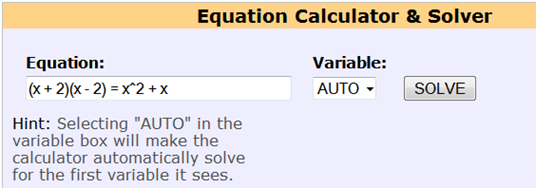
Provate a confrontare queste due immagini:
Secondo voi un alunno di prima media è in grado di risolvere un sistema formato da 3 incognite e 3 equazioni lineari?
La sfida consiste proprio nel riuscire a rendere facile e divertente questo genere di problemi.
Come?
Il sito che vi proponiamo ci prova e, secondo noi, ci riesce bene!
Come tutti i giochi anche Solvemoji permette di scegliere tra 5 livelli di difficoltà (Facile, Medio, Difficile, Esperto e il terribile “Master”).
Se rimanete bloccati potete sempre cliccare sul pulsante “Rivela la soluzione”, ma perderete punti ed onore ![]()
Non è necessario registrarsi, ma se decidete di farlo potrete partecipare alla sfida globale e cercare di entrare nella graduatoria dei migliori in assoluto!
Terminiamo questa presentazione illustrando la soluzione, un passo alla volta, del problema presentato all’inizio:
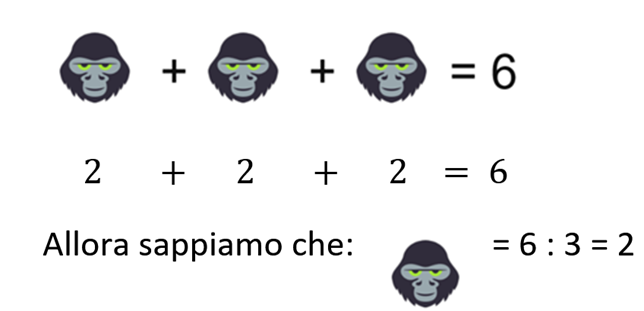
Nella prima riga vediamo che 3 scimmioni valgono 6, possiamo dedurre che uno scimmione vale 6 : 3 = 2
Nella seconda riga vediamo che una tigre e due scimmioni valgono 16
Allora se togliamo i due scimmioni sia da sinistra che da destra:
Scopriremo che una tigre vale:
Nella terza riga abbiamo due tigri ed un facocero che insieme valgono 33
Anche in questo caso per scoprire quanto vale un facocero possiamo togliere le tigri (e il loro valore) da entrambe le parti dell’equazione:
Adesso sappiamo che un facocero vale:
Abbiamo scoperto i valori di tutti gli animaletti!
e possiamo finalmente sapere il valore che ci viene chiesto nell’ultima riga:
dove vediamo due facoceri da sommare ad una tigre moltiplicata per due scimmioni: