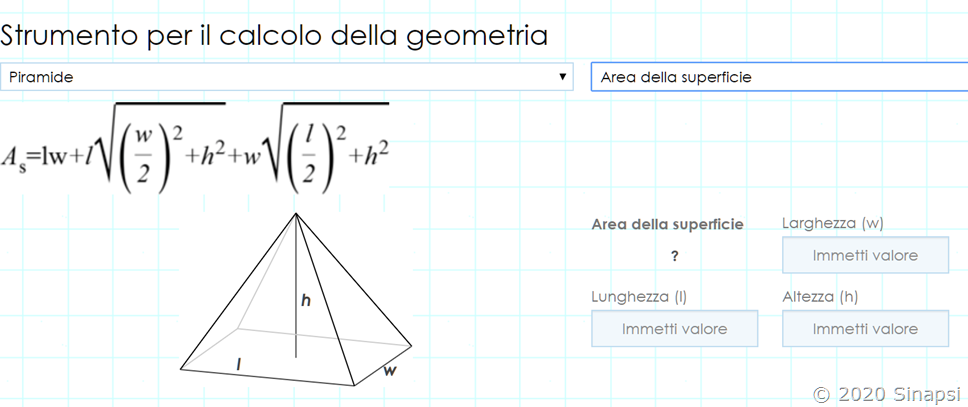
Abbiamo trovato e riadattato questo strumento che ci permette di risolvere molti problemi di geometria piana e solida.
Precisamente potrete trovare: diagonali, perimetri, raggi, diametri, basi, altezze, aree e volumi.
Geometria piana:
Cerchio
Ellisse
Esagono
Ettagono
Ottagono
Parallelogramma
Pentagono
Quadrato
Rettangolo
Rombo
Trapezio
Triangolo (equilatero, isoscele e rettangolo)
Geometria solida:
Cilindro
Cono
Cubo
Ottaedro
Piramide
Prisma (rettangolare e triangolare)
Sfera
Tetraedro
Il suo utilizzo è molto semplice, basta inserire i dati conosciuti nelle relative caselle e otterrete immediatamente la risposta.
Vi consigliamo di verificare la correttezza dei risultati utilizzando le formule che compaiano a fianco.