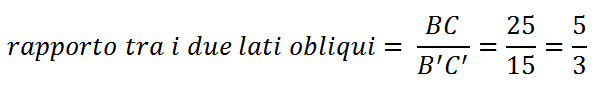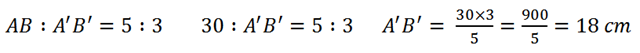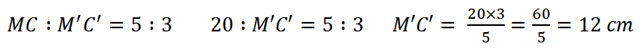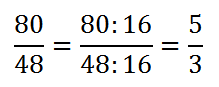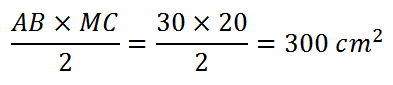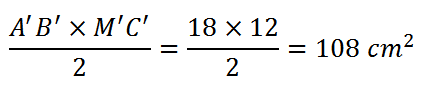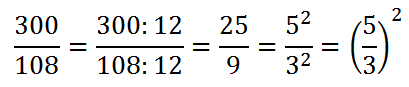Un nostro lettore ci ha inviato questo problema di seconda media:

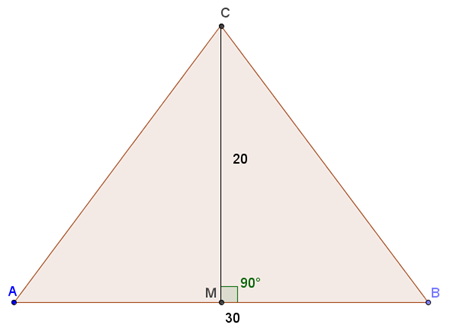
Un triangolo isoscele ha la base lunga 30 cm e l’altezza ad essa relativa lunga 20 cm.
Calcola l’area di un triangolo simile a quello dato sapendo che il lato obliquo del secondo triangolo misura 15 cm.
Quanto vale il rapporto fra le aree? e quello dei perimetri?

Soluzione:

Iniziamo disegnando il triangolo.

  Dove AB=30 e MC=20.

Troviamo la misura dei due lati obliqui applicando il teorema di Pitagora al triangolo rettangolo MBC. Calcoliamo quindi l’ipotenusa BC sapendo che il cateto minore misura MB=30:2=15 cm mentre il cateto maggiore misura MC=20 cm

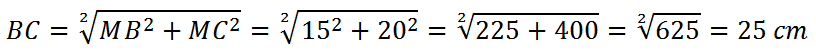Sapendo che il lato obliquo del secondo triangolo B’C’ = 15 cm possiamo sapere il rapporto di similitudine.

Allora troviamo la misura della base e dell’altezza del secondo triangolo, risolvendo queste proporzioni.

Per cui il secondo triangolo avrà queste misure: A’B’ = 18 cm;  A’C’ = B’C’ = 15 cm; M’C’ = 12 cm

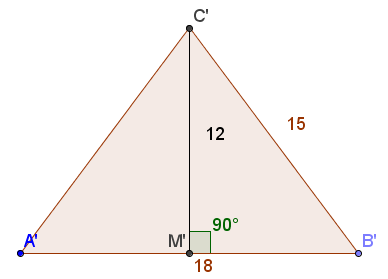Troviamo i due perimetri e le due aree.

Perimetro primo triangolo: AB + BC + AC = 30 + 25 + 25 = 80 cm

Perimetro del secondo triangolo: A’B’ + B’C’ + A’C’ = 18 + 15 + 15 = 48 cm 

Si osserva che il rapporto tra i due perimetri, una volta semplificato, è uguale al rapporto tra i lati:

Area primo triangolo:

Area secondo triangolo:

Osserviamo che il rapporto tra le aree, una volta semplificato, è il quadrato del rapporto tra lati e perimetri:

c.v.d.