Archivi tag: come fare per

Dimostrazione geometria piana

Lascia una risposta

clip_image002[6]

Dato il trapezio in figura, dimostrare che:

DC=AD+BC  e l’angolo DOC =90°

Dimostrazione

1) Sappiamo, per la nota proprietà, che i segmenti di tangente DT=AD e TC=BC quindi sommando membro a membro abbiamo che: DT+TC= AD+BC, ma DT+TC=DC quindi DC=AD+BC

2) I triangoli ADO e DOT sono congruenti perché hanno entrambi l’angolo retto clip_image006[7] inoltre hanno i lati AD=DT perché segmenti di tangente e i due lati AO=OT perché entrambi raggi della stessa circonferenza. Quindi in particolare sono uguali gli angoli

clip_image008[7]

Stesso ragionamento per i triangoli OTC=OCB che hanno uguali gli angoli

clip_image010[7]

Osserviamo che l’angolo clip_image012[7] ed è formato da clip_image014[7]la somma delle rispettive metà vale:

clip_image016[7]

Ma le rispettive metà sono proprio: clip_image018[7] c.v.d.

Problema di geometria su segmenti e settori circolari

1 Replica

Problema:

Una corda di circonferenza, lunga 24 pi greco cm, misura 12 cm. Determina l’area dei due segmenti circolari individuati dalla corda ab e dall’arco ab .

Soluzione:

Questa è la figura. Il segmento circolare piccolo è quello colorato di giallo, l’altro è la somma della parte azzurra e del triangolo arancione.

clip_image004[4]

Osserva che AOC è un triangolo equilatero avendo AC = AO = CO = 12 cm

DO è la distanza della corda dal centro ed è anche l’altezza del triangolo equilatero.

Altezza del triangolo equilatero clip_image006[5]

DO = 0,866 x 12 = 10,39 cm

Se noi calcoliamo l’area del settore circolare AOC (giallo + azzurro) e ci togliamo l’area del triangolo equilatero arancione sapremo la misura dell’area del segmento circolare giallo.

L’angolo AOC misura 60° perché è l’angolo interno di un triangolo equilatero, allora il settore circolare AOC (giallo più azzurro) ha l’area che vale la sesta parte di quella del cerchio. (60° è la sesta parte di 360°). Se preferisci puoi usare la proporzione:

settore : angolo = cerchio : 360°

clip_image008[5]

clip_image010[5]

L’area del triangolo equilatero si calcola con base per altezza diviso due:

clip_image012[5]

Infine troviamo l’area del segmento circolare giallo = area del settore circolare – area del triangolo:

75,36 – 62,34 = 13,02 cm2

Mentre l’area del segmento circolare grande (arancione + azzurro) è uguale a:

area cerchio – area segmento circolare piccolo giallo

clip_image014[6]

clip_image016

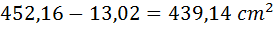
Risposta:

Area segmento circolare piccolo giallo = 13,02 cm2

Area segmento circolare grande arancio + azzurro = 439,14 cm2