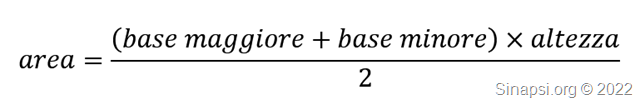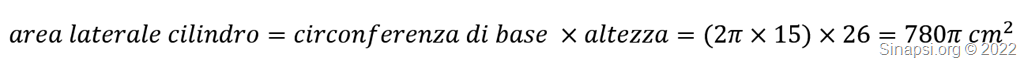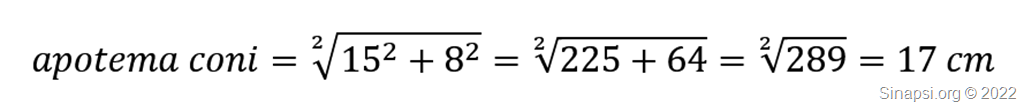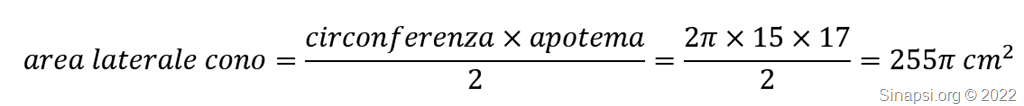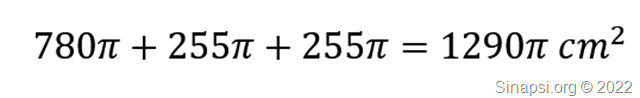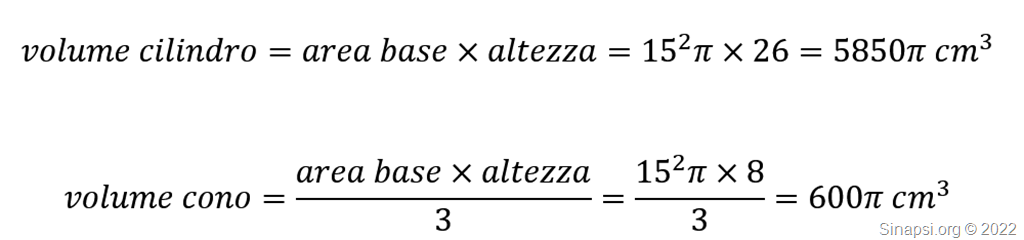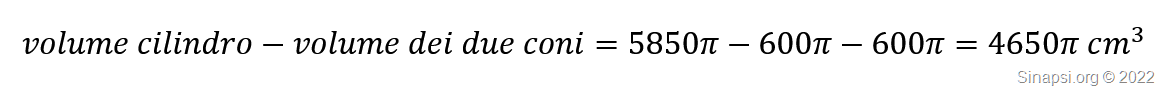Esercizio N° 196 La somma delle basi di un trapezio isoscele è di 36 cm e la base maggiore supera la minore di 16 cm. Sapendo che l’area del trapezio misura 270 cm2, determina l’area della superficie totale e il volume del solido che si ottiene facendo ruotare il trapezio di 360° intorno alla base minore.

Quando conosciamo la somma e la differenza di due valori possiamo procedere così (vedi nostro post):
- Togliamo dalla somma la differenza (36 – 16 = 20)
- Dividiamo per 2 il risultato (20 : 2 = 10) per ottenere il valore del numero più piccolo
- Sommiamo al numero piccolo la differenza (10 + 16 = 26) per ottenere il valore del numero più grande
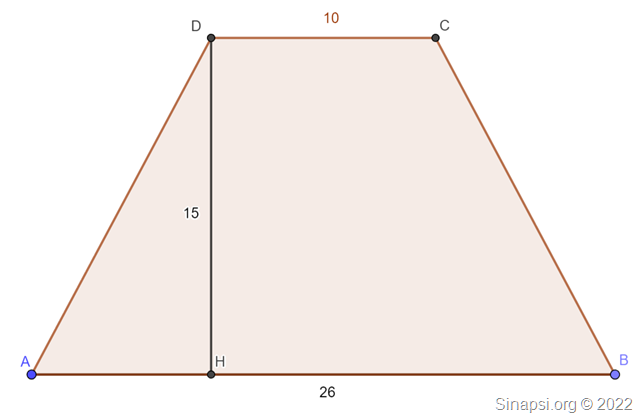
Quindi la base maggiore misura 26 cm mentre la base minore misura 10 cm.
Adesso calcoliamo l’altezza del trapezio usando la formula inversa dell’area.
Ricordiamo che l’area del trapezio si calcola con questa formula:
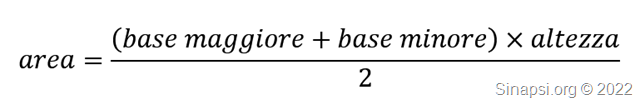
Per cui la formula inversa ci permette di calcolare l’altezza:

Questo è il nostro trapezio isoscele.
Se adesso facciamo ruotare di 360° il trapezio attorno alla sua base minore otteniamo questo solido. Si tratta di un cilindro con due cavità coniche.
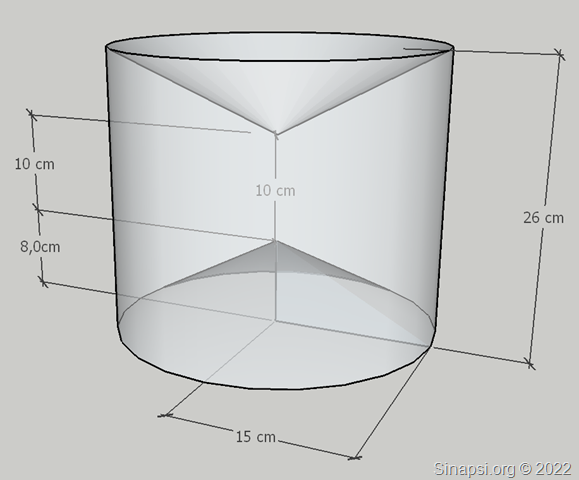
Per calcolare l’area della superficie totale di questo solido di rotazione dobbiamo sommare quella laterale del cilindro e quelle laterali dei due coni.
Il cilindro è alto 26 cm ed ha il raggio di base di 15 cm.
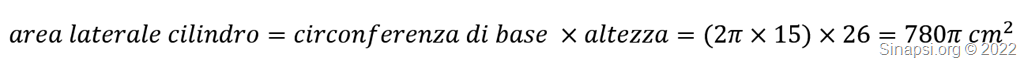
I due coni (uguali) hanno il raggio di base sempre di 15 cm, il loro apotema si calcola con Pitagora:
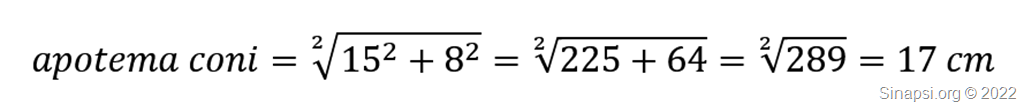
Quindi l’area laterale del cono si trova così:
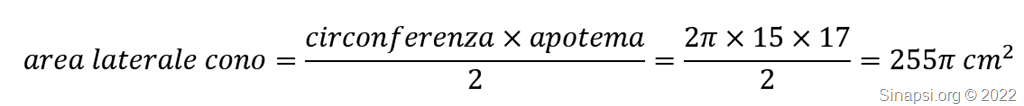
Ora basta sommare le tre aree laterali per trovare l’area totale del solido:
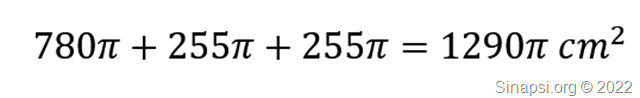
Il volume è formato dal quello del cilindro a cui dobbiamo sottrarre le due cavità formate dai due coni.
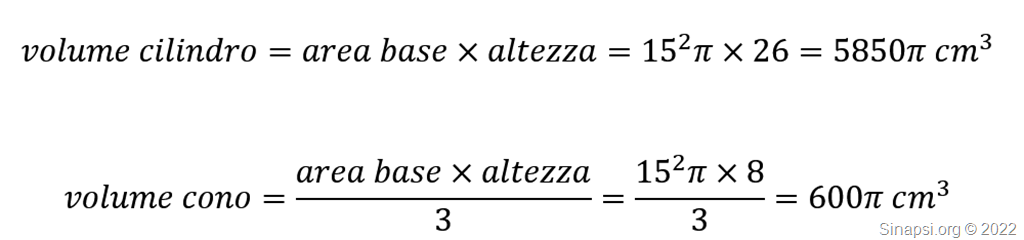
Volume totale del solido di rotazione:
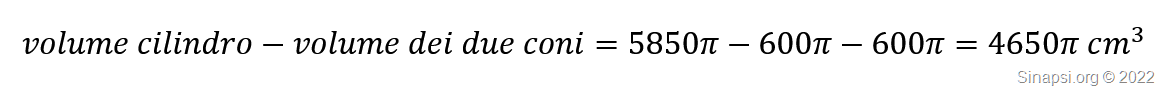
Mi piace:
Mi piace Caricamento...