Archivi tag: Geometria

Piramide con base un rombo, problema risolto

4 Repliche

Problema:

Una piramide retta ha per base un rombo la cui area misura 1536 cm². Sapendo che una diagonale è i 24/32 dell’altra e che l’altezza della piramide è uguale all’altezza di un parallelepipedo rettangolo che ha le due dimensioni di base e il volume rispettivamente di 42 cm, 30 cm e 32256 cm³, calcola l’area della superficie totale e il volume della piramide.

image

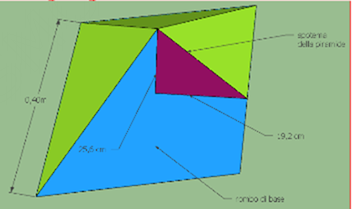
Questo è un tipico problema assegnato all’esame di terza media.

Vi proponiamo una soluzione integrata da disegni realizzati con GeoGebra (immagine 2D) e con SketchUp (immagine 3D).


Qui sotto potete interagire con la figura in 3D. (abbiate pazienza e aspettate che si carichi)

Dimostrazione geometria piana

Lascia una risposta

clip_image002[6]

Dato il trapezio in figura, dimostrare che:

DC=AD+BC  e l’angolo DOC =90°

Dimostrazione

1) Sappiamo, per la nota proprietà, che i segmenti di tangente DT=AD e TC=BC quindi sommando membro a membro abbiamo che: DT+TC= AD+BC, ma DT+TC=DC quindi DC=AD+BC

2) I triangoli ADO e DOT sono congruenti perché hanno entrambi l’angolo retto clip_image006[7] inoltre hanno i lati AD=DT perché segmenti di tangente e i due lati AO=OT perché entrambi raggi della stessa circonferenza. Quindi in particolare sono uguali gli angoli

clip_image008[7]

Stesso ragionamento per i triangoli OTC=OCB che hanno uguali gli angoli

clip_image010[7]

Osserviamo che l’angolo clip_image012[7] ed è formato da clip_image014[7]la somma delle rispettive metà vale:

clip_image016[7]

Ma le rispettive metà sono proprio: clip_image018[7] c.v.d.