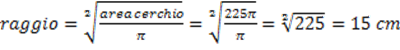Una nostra lettrice, che si firma Lola99, ci invia questo problema di geometria solida, tipico della classe terza media. Ecco come risolverlo, un passaggio alla volta.

Problema: Un solido è formato da un cilindro sormontato da un cono avente per base una base del cilindro. Determina l’altezza del solido sapendo che la sua superficie è 565,2 centimetri quadrati, la circonferenza di base misura 47,1 centimetri e l’altezza del cilindro è di 4 centimetri.

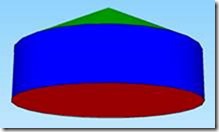
Soluzione: L’area laterale del cilindro (colore blu) è = circonferenza x altezza = 47,1 x 4 = 188,4 cm²

Sapendo la circonferenza possiamo trovare il raggio

Troviamo l’area del cerchio di base (colore rosso)

Per trovare l’area laterale del cono (colore verde) togliamo dalla superficie di tutto il solido la superficie laterale del cilindro e l’area del cerchio di base.

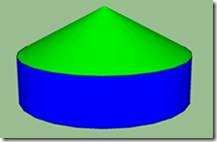
Area laterale cono (verde) = area totale – area cerchio base (rosso) – area laterale cilindro (blu)=

= 565,2 – 188,4 – 176,625 = 200,175 cm²

Troviamo l’apotema del cono

Con Pitagora troviamo l’altezza del cono

Altezza di tutto il solido = altezza cilindro + altezza cono = 4 + 4 = 8 cm