Oggi vi mostriamo i passaggi che ci permettono di trovare il valore dell’incognita x in un’equazione di primo grado, una di quelle che dovrete risolvere nel prossimo esame di terza media.
Procedimento:
(il filmato si carica in pochi secondi)
Oggi diamo la soluzione di un problema di geometria analitica, uno di quelli che potrebbero capitare agli esami di terza media.
Questo è il testo, provate a risolverlo da soli e cliccate qui solamente se volete vedere la soluzione completa.
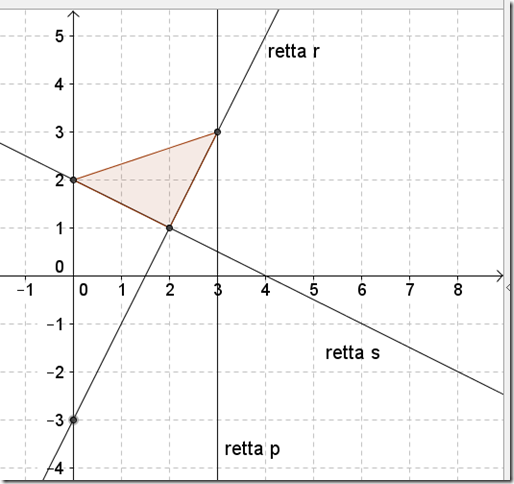
Problema:
a) Partendo dall’equazione generale delle rette y = mx + k, scrivi l’equazione della retta r di coefficiente angolare m = 2, passante per il punto A(0; –3) e rappresentala graficamente in un riferimento cartesiano, assumendo una unità di misura a piacere.
b) Scrivi l’equazione della retta s passante per il punto C (0; 2) e perpendicolare alla retta r nel punto B.
c) Determina graficamente le coordinate del punto B; calcola l’area del triangolo CBD, essendo D il punto in cui la retta p di equazione x = 3 incontra la retta r.