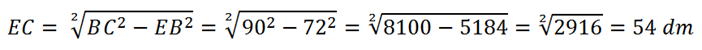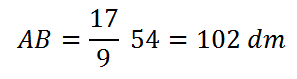Archivi tag: soluzione

Risolviamo un problema di geometria

2 Repliche

Oggi risolviamo il problema di Matteo.

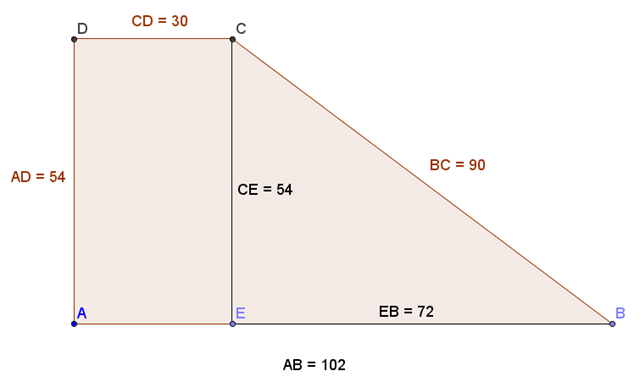
Un trapezio rettangolo il lato obliquo è 90 dm, la sua proiezione sulla base maggiore 72 dm.

Sapendo che la base maggiore è 17/9 dell’altezza, calcola la misura del lato di un rombo isoperimetrico al trapezio.

Soluzione

image

Con teorema di Pitagora troviamo l’altezza del trapezio EC

image

 

 

Se la base maggiore AB è 17/9 dell’altezza:

image

 

 

 

Se il rombo ha lo stesso perimetro del trapezio, calcoliamo il perimetro del trapezio:

AB+BC+CD+AD=102+90+30+54=276 dm

Quindi il lato del rombo, che ha 4 lati uguali, misura 276:4=69 dm     c.v.d.

Mi aiutate a risolvere questo problema di geometria?

Come sapete il sito answers.yahoo.com abbonda di appelli disperati di studenti che vogliono la soluzione immediata del compito di matematica o geometria.

Ne abbiamo risolto uno relativo a triangoli simili.

Problema di geometria

Il perimetro di un triangolo isoscele è 60 dm e il lato obliquo è i 4/7 della base. Calcola il perimetro di un triangolo isoscele simile sapendo che la sua base è di 112 dm.

Soluzioneclip_image002

Il perimetro è formato da AB+BC+AC e corrisponde a 4/7+4/7+7/7=15/7

Sappiamo che il perimetro misura 60 dm che quindi corrisponde a 15/7

Se 15/7 corrispondono a 60 dm allora 1/7 corrisponde a 60/15 = 4 dm

Quindi se AC è i 4/7 abbiamo che AC = BC = 4 * 4 = 16 dm mentre AB = 4*7 = 28 dm

Verifica: AB+BC+AC=16+16+28 = 60 dm

Il triangolo simile ha la base di 112 dm, quindi è 112/28 = 4 volte più grande del primo.

Anche il perimetro del triangolo simile è 4 volte più grande: 60*4 = 240 dm c.v.d.

[Se vuoi aiuto per altri problemi, clicca qui.]