Abbiamo parlato numerose volte di come sia efficace insegnare la geometria con gli strumenti dinamici.
Vediamo come sia possibile verificare graficamente i due teoremi di Euclide.
Le costruzioni realizzate con GeoGebra sono interattive.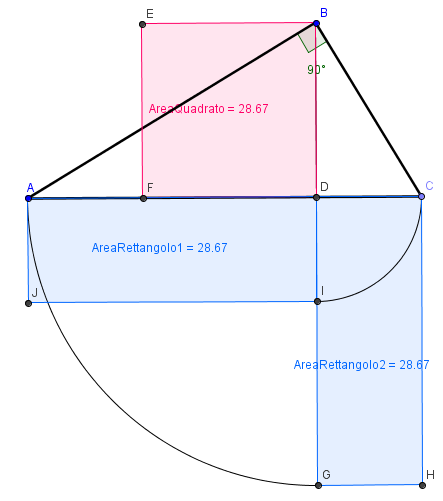
Sposta i vertici dei triangoli rettangoli con il mouse e ti renderai conto delle equivalenze tra quadrati e rettangoli colorati.
Verifica il primo teorema di Euclide muovendo uno dei vertici del triangolo rettangolo ABC.
In un triangolo rettangolo ABC il quadrato costruito su un cateto (ABJK rosso o BCEF blu) è equivalente al rettangolo (ADIH rosso o DCGI blu) avente per dimensioni l’ipotenusa e la proiezione di quel cateto sull’ipotenusa stessa.
Verifica il secondo teorema di Euclide muovendo uno dei vertici del triangolo rettangolo ABC.
Il quadrato BDFE (rosso) costruito sull’altezza relativa all’ipotenusa (BD) è equivalente al rettangolo ADIJ o DCHG (azzurro) che ha come dimensioni le proiezioni dei cateti sull’ipotenusa: AD e DC
Mi piace:
Mi piace Caricamento...


