Archivi tag: come fare per

Come faccio a risolvere questo problema di geometria?

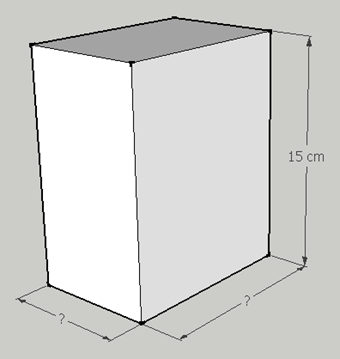
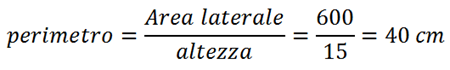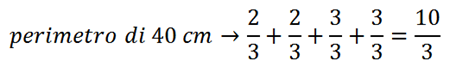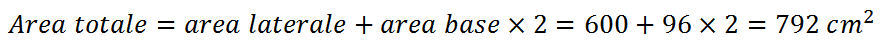Problema: L’area di un cerchio è di 452,16 cm2. Da un punto P distante 15 cm dal centro, conduci le 2 tangenti AP e PB. Trova il perimetro e l’area del quadrilatero OAPB.

Soluzione:

Sapendo che l’area del cerchio si trova: clip_image002[6]

Troviamo il raggio con la formula inversa:

clip_image004[6]

Possiamo disegnare la figura:

clip_image006[6]

I triangoli PBO e PAO sono rettangoli perché le tangenti sono perpendicolari ai raggi BO e AO.

Applichiamo il Teorema di Pitagora per trovare i cateti BP=AP

clip_image008[6]

Quindi il perimetro del quadrilatero AOBP è la somma dei suoi lati:

clip_image010[6]

Mentre l’area del quadrilatero AOBP è la somma delle aree dei due triangoli AOP e BOP:

clip_image012[6]

clip_image014[6]

c.v.d.

Se vuoi un aiuto personalizzato per risolvere un problema di geometria, un’espressione con frazioni e potenze, clicca qui.

Geometria solida, problema di terza media risolto

8 Repliche

Un lettore scrive:

L’area della superficie laterale di un parallelepipedo rettangolo è di 600 cm quadrati.
Calcola l’area della superficie totale del parallelepipedo, sapendo che le dimensioni di base sono una i 2/3 dell’altra e che la sua altezza misura 15 cm

Questa è l’immagine del solido.

image

Se conosciamo area laterale ed altezza possiamo calcolare il perimetro di base.

image Conosciamo il rapporto tra le dimensioni di base, quindi se una è i due terzi, l’altra è i tre terzi e il perimetro corrisponde a dieci terzi.

imageallora ognuno dei dieci terzi corrisponde a 4 cm per cui la misura di due terzi vale 4 x 2 = 8 cm mentre l’altra vale 4 x 3 = 12 cm

Come verifica controlliamo: 8+8+12+12=40 cm e inoltre 8 è i due terzi di 12.

Adesso possiamo calcolare l’area della base.

imagee l’area totale.

image