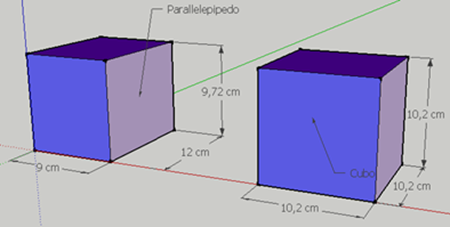
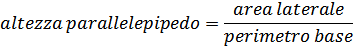Un nostro visitatore ci scrive:

ciao, scusa ho 13 anni e frequento la 3 media, vorrei chiederti una spiegazione più approfondita delle espressioni algebriche con le frazioni e se possibile anche con gli elevamenti a potenza.

Affrontiamo insieme questa:

risolviamo le parentesi tonde:

sommiamo i monomi simili:

calcoliamo il minimo comune multiplo dei denominatori:

sostituiamo ciascun denominatore con il m.c.m.=30 e moltiplichiamo ciascuna nuova frazione per il risultato della divisione tra m.c.m. e denominatore originale: ad esempio nella prima frazione abbiamo 30 diviso 5=6:

moltiplico per ciascun monomio presente al numeratore di ogni frazione:

moltiplico entrambi i membri dell’equazione per 30, in tal modo posso semplificare ed eliminare i denominatori:

adesso sommo i monomi simili:

e porto a sinistra del simbolo di uguale i monomi con la “x” e a destra i numeri senza la “x”:

ancora sommo i monomi simili:

divido entrambi i membri dell’equazione per 3:

questo è il risultato dell’equazione: