Archivi tag: Geometria

Problema con trapezio rettangolo, seconda media

4 Repliche

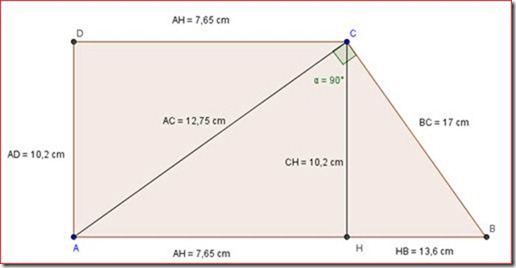
Il problema dice: "In un trapezio rettangolo la diagonale minore è perpendicolare al lato obliquo e quest’ultimo misura 17 cm. Calcola il perimetro e l’area dei due triangoli in cui la diagonale minore divide il trapezio sapendo che la differenza delle due basi misura 13,6 cm.

clip_image002

Soluzione.

Applico il teorema di Pitagora al triangolo HBC:

clip_image004

Applico il teorema di Euclide al triangolo ABC:

HB : HC = HC : AH 13,6 : 10,2 = 10,2 : AH

clip_image006

AB = AH + HB = 7,65 + 13,6 = 21,25 cm

Applico il teorema di Pitagora al triangolo ABC:

clip_image008

Perimetro triangolo ABC = AB + BC + AC = 21,25 + 17 + 12,75 = 51 cm

Area triangolo ABC = clip_image010

Perimetro triangolo ACD = AC + CD + DA = 12,75 + 7,65 + 10,2 = 30,6 cm

Area triangolo ACD = clip_image012

c.v.d.

Come faccio a risolvere questo problema di geometria?

Problema: L’area di un cerchio è di 452,16 cm2. Da un punto P distante 15 cm dal centro, conduci le 2 tangenti AP e PB. Trova il perimetro e l’area del quadrilatero OAPB.

Soluzione:

Sapendo che l’area del cerchio si trova: clip_image002[6]

Troviamo il raggio con la formula inversa:

clip_image004[6]

Possiamo disegnare la figura:

clip_image006[6]

I triangoli PBO e PAO sono rettangoli perché le tangenti sono perpendicolari ai raggi BO e AO.

Applichiamo il Teorema di Pitagora per trovare i cateti BP=AP

clip_image008[6]

Quindi il perimetro del quadrilatero AOBP è la somma dei suoi lati:

clip_image010[6]

Mentre l’area del quadrilatero AOBP è la somma delle aree dei due triangoli AOP e BOP:

clip_image012[6]

clip_image014[6]

c.v.d.

Se vuoi un aiuto personalizzato per risolvere un problema di geometria, un’espressione con frazioni e potenze, clicca qui.