Proponete questo problema di geometria ai vostri studenti o risolvetelo da soli senza andare subito alla soluzione.

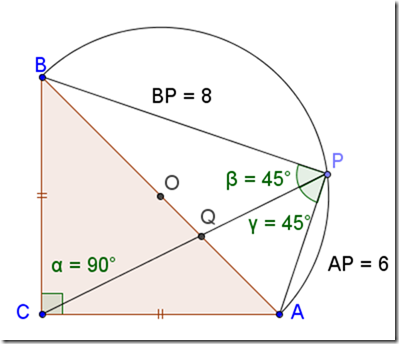
Problema: Sia ABC un triangolo rettangolo, isoscele sulla base AB. Nel semipiano avente come origine la retta AB cui non appartiene C, traccia la semicirconferenza di diametro AB. Considera un punto P sulla semicirconferenza e indica con Q il punto di intersezione di AB e PC.

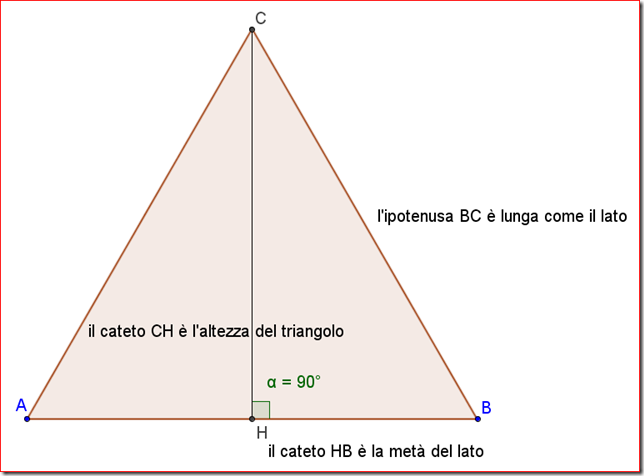
a) Dimostra che la semiretta PC è la bisettrice dell’angolo APB.

b) Supposto che AP=6 cm e BP=8 cm, determina le misure di AQ e QB nonché il perimetro e l’area del quadrilatero ACBP.

Vai alla Soluzione