Un nostro lettore ci invia un problema di terza media che coinvolge la superficie laterale di un cono vista come settore circolare.
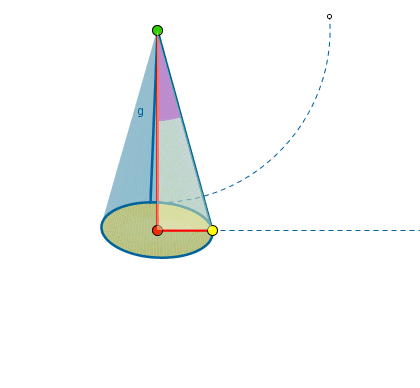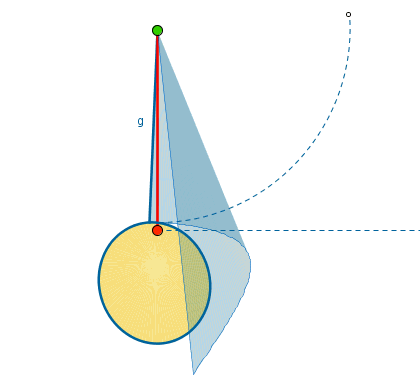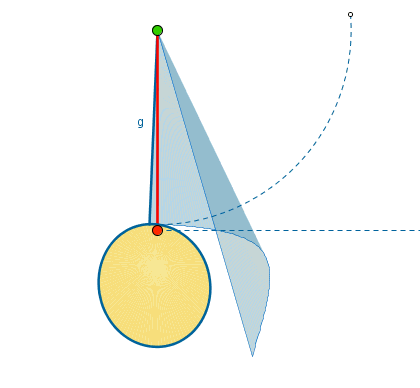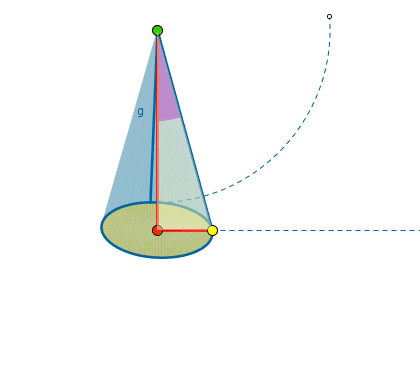
Per meglio comprendere come risolvere questo genere di problemi osserviamo questa immagine animata.
Come vedete il settore circolare che si ottiene sviluppando sul piano l’area laterale ha come raggio l’apotema del cono e l’arco è lungo quanto la circonferenza di base.
Problema: Determinare il volume di un cono la cui superficie laterale si sviluppa in un settore circolare di 120° e raggio 12 cm.
Soluzione: Tutta la circonferenza di raggio = 12 cm misura
![]()
Troviamo la lunghezza dell’arco AB impostando e risolvendo la proporzione:
120° : AB = 360° : 75,36
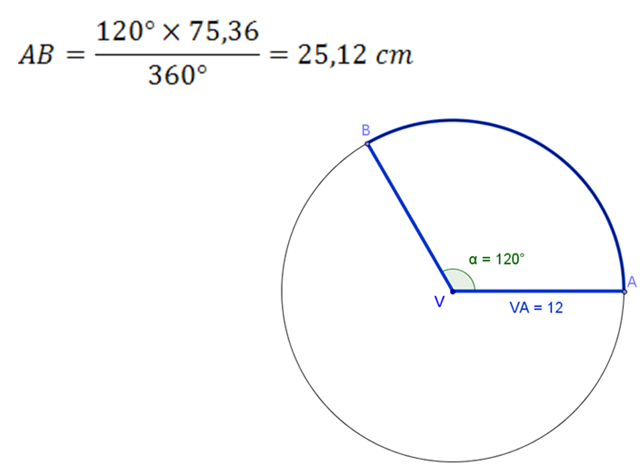
L’arco AB è la circonferenza di base del cono.
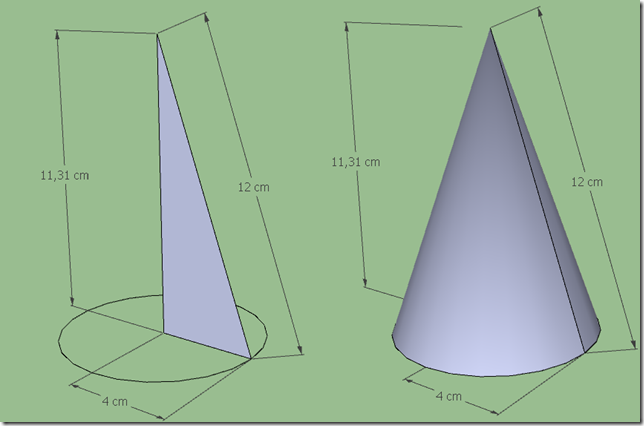
Di cui possiamo calcolare il raggio di base con la formula inversa:

Troviamo l’altezza del cono con Pitagora.