Un nostro lettore ci invia un problema di terza media che coinvolge la superficie laterale di un cono vista come settore circolare.
Per meglio comprendere come risolvere questo genere di problemi osserviamo questa immagine animata.
Come vedete il settore circolare che si ottiene sviluppando sul piano l’area laterale ha come raggio l’apotema del cono e l’arco è lungo quanto la circonferenza di base.
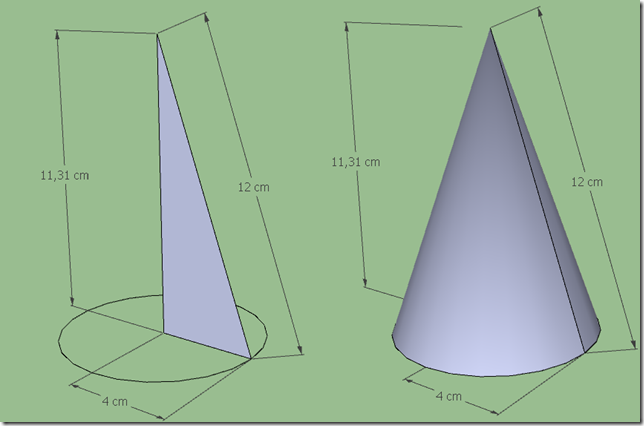
Problema: Determinare il volume di un cono la cui superficie laterale si sviluppa in un settore circolare di 120° e raggio 12 cm.
Soluzione: Tutta la circonferenza di raggio = 12 cm misura
![]()
Troviamo la lunghezza dell’arco AB impostando e risolvendo la proporzione:
120° : AB = 360° : 75,36
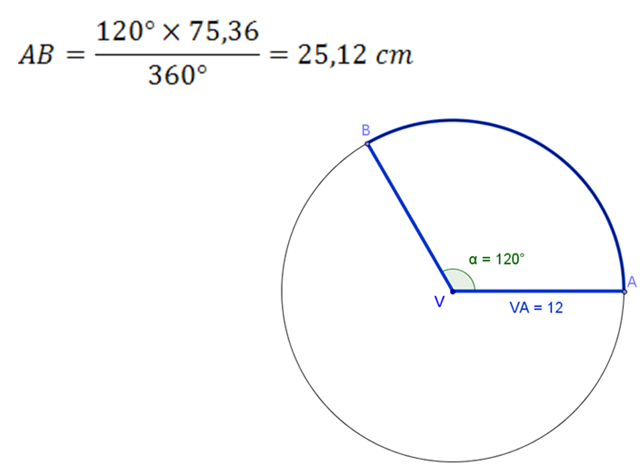
L’arco AB è la circonferenza di base del cono.
Di cui possiamo calcolare il raggio di base con la formula inversa:

Troviamo l’altezza del cono con Pitagora.


Caro Michele, ti aiuteremo molto volentieri se inserirai il tuo quesito nella sezione “geometria” del nostro blog. Clicca qui per arrivarci.
A presto.
p.s. purtroppo il tuo problema prevede la costruzione di coniche, argomento che esula dall’ambito del nostro blog (scuola media inferiore)
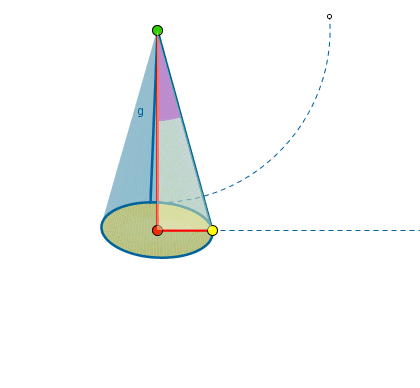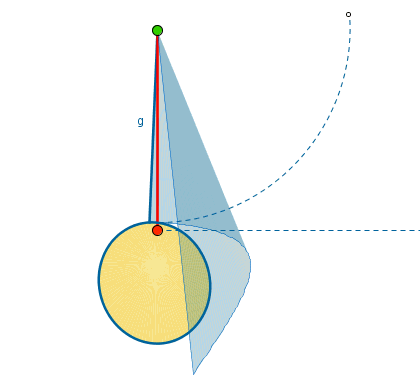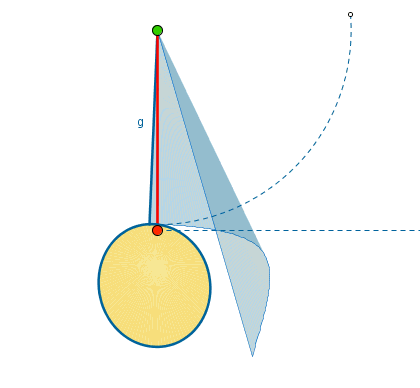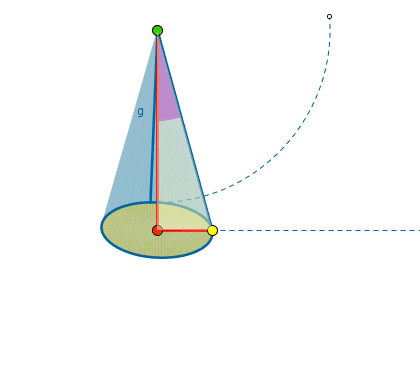
per fare la cappa del mio camino dovrei sviluppare un solido a forma di cono con base ellittica con le seguenti misure:
h= 210 cm, ellisse di base : asse maggiore 170 cm, asse minore 100 cm. A 210 cm dalla base l’ellisse deve avere un’asse minore non più di 34 cm.
Potete, per favore aiutarmi a costruire lo sviluppo del tronco di cono?. Alla fine, la cappa sarà formata dal tronco di cono tagliato a metà in modo da avere un semi tronco alto 210 cm, largo 100 cm e profondo 85 cm.
Vi ringrazio anticipatamente e invio cordiali saluti
michele babbini