Verificare il primo teorema di Euclide, con GeoGebra

Venerdì scorso ho introdotto il primo teorema di Euclide agli studenti di terza:

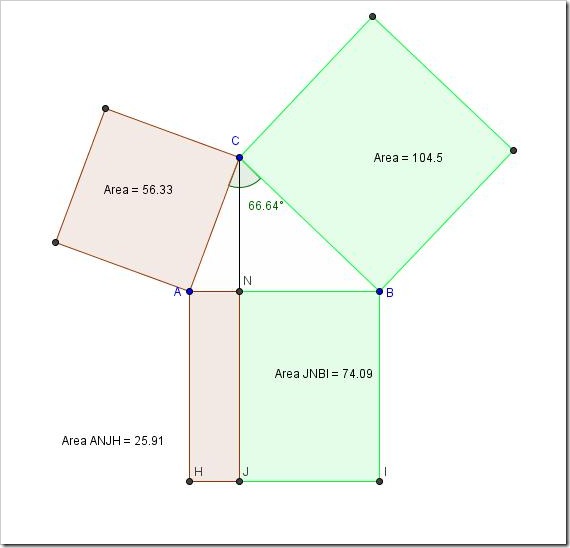
In un triangolo rettangolo, il quadrato costruito su un cateto è equivalente al rettangolo avente per dimensioni l’ipotenusa e la proiezione di quel cateto sull’ipotenusa.

Il solito Marco, insieme ad Alberto, mi ha chiesto, osservando la figura:

Ma se lasciamo fissa la lunghezza dell’ipotenusa AB e modifichiamo solo l’altezza CN allora cambiano solo i quadrati! Come possono restare equivalenti ai due rettangoli?

Dopo un attimo di perplessità, gli stessi Marco ed Alberto hanno suggerito la risposta.

Trovatela anche voi muovendo il punto C nella figura interattiva qui sotto:

Euclide Uno – GeoGebra Foglio di lavoro dinamico

Autore: Daniele

Ho insegnato matematica e scienze alle medie a Genova, Addis Abeba e Barcellona. Mi piace scovare giochi didattici dedicati alla matematica. Io e Luvi abbiamo viaggiato in Europa, India, Tibet, Nepal, Cina, Australia, Indonesia, Birmania, Tailandia, Sri Lanka, Perù, Messico, Guatemala, Belize, Etiopia, Marocco, Egitto, Congo, Ruanda, Mali, Costa d'Avorio, Togo, Ghana e qualche altro posto.Mi trovi su Instagram Vedi tutti gli articoli di Daniele