Risolviamo insieme questo problema di geometria inviatoci da un nostro lettore.
Problema: In un trapezio rettangolo ABCD, la base minore e l’altezza sono congruenti, sapendo che l’area è 378 cm2 e che la base maggiore è 4/3 della base minore, calcola la misura delle due basi e dell’altezza.
Soluzione: Se disegniamo la figura possiamo capire che…
il rettangolo AEFD, formato dal doppio del nostro trapezio ABCD, ha un’area di 378 x 2 = 756 cm2 ed è formato da 21 quadratini.
Allora l’area di ognuno dei 21 quadratini misura 756 : 21 = 36 cm2.
Se l’area di ogni quadratino misura 36 cm2, il suo lato è lungo:
![]() Infine, essendo la base maggiore AB formata da 4 quadratini, sarà lunga 6 x 4 = 24 cm.
Infine, essendo la base maggiore AB formata da 4 quadratini, sarà lunga 6 x 4 = 24 cm.
Mentre l’altezza AD e la base minore DC, essendo formate da 3 quadratini, saranno 3 x 6 = 18 cm.
Risposta: base maggiore AB = 24 cm; altezza AD e base minore DC = 18 cm.
Verifica:
![]()

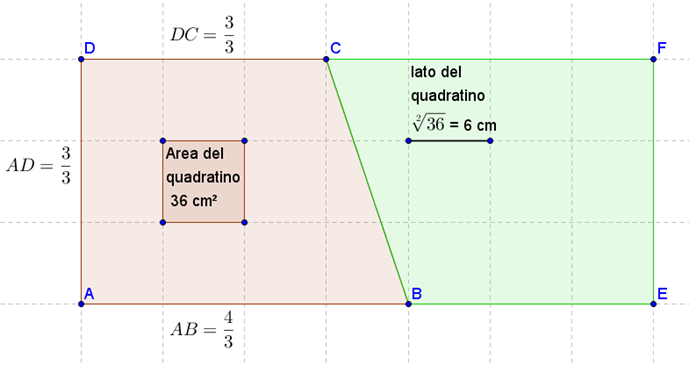
Se guardi la figura vedi che il rettangolo ha la base formata da 7 segmenti e l’altezza da 3, quindi 7 x 3 = 21. Ciao
Perché 21 quadratini? Come si calcolano?