Problema che potrebbe capitare alla prova scritta di matematica per la Terza Media.

Disegniamo il trapezio isoscele per capire come calcolarne l’altezza.
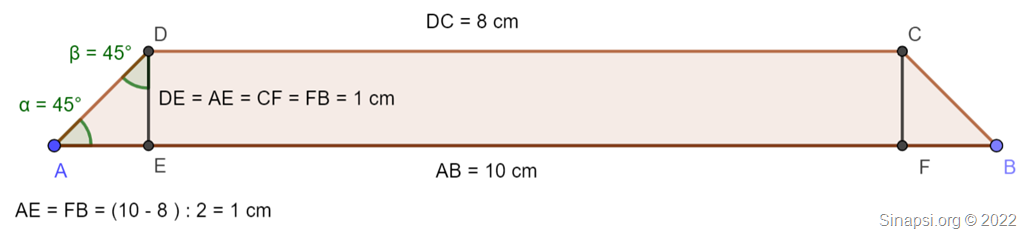
L’altezza del trapezio DE è uguale ai segmenti AE e DE perché il triangolo ADE è rettangolo e anche isoscele avendo gli angoli α e β entrambi di 45°. Inoltre AE = FB perché il trapezio è isoscele e misurano (AB – DC) : 2 = (10 – 8) : 2 = 1 cm
Quindi l’altezza del trapezio misura 1 cm.
Per trovare la superficie totale di questo prisma dobbiamo sommare le aree delle due basi trapezoidali all’area laterale.
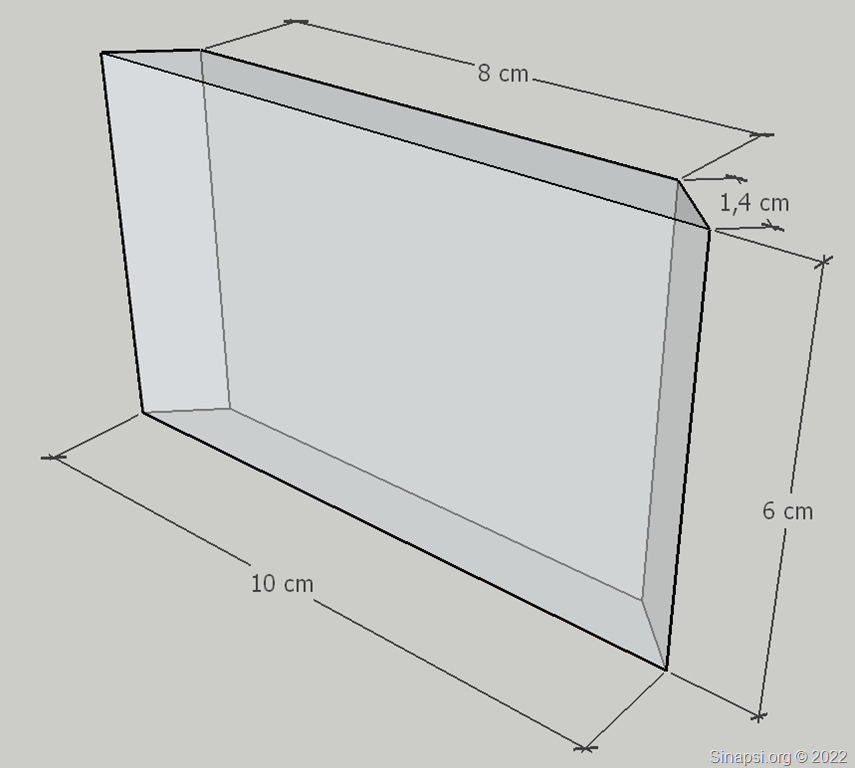
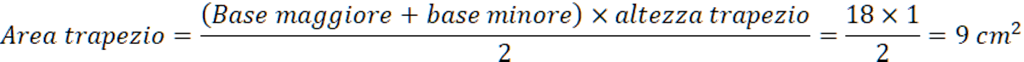
L’area laterale del prisma si ottiene moltiplicando il perimetro del trapezio per l’altezza del prisma:
Per calcolare il perimetro del trapezio isoscele troviamo il lato obliquo con Pitagora:
![clip_image002[10] clip_image002[10]](https://www.sinapsi.org/wordpress/wp-content/uploads/2022/09/clip_image00210.png)
Perimetro = AB+BC+CD+DA=10+1,4142+8+1,4142=20,8284 cm
Area laterale = perimetro x altezza del prisma = 20,8284 x 6 = 124,9704 cm2
Area totale = area delle due basi + area laterale = 9 + 9+ 124,9704 = 142,9704 cm2
